| | Some definitions of interest. |
|
| msga | Def MsgA
Def == ds:x:Id fp-> Type
Def ==  da:a:Knd fp-> Type da:a:Knd fp-> Type
Def ==  x:Id fp-> ds(x)?Void x:Id fp-> ds(x)?Void a:Id fp-> State(ds) a:Id fp-> State(ds)  ma-valtype(da; locl(a)) ma-valtype(da; locl(a))  Prop Prop
Def == kx:Knd Id fp-> State(ds) Id fp-> State(ds)  ma-valtype(da; 1of(kx)) ma-valtype(da; 1of(kx))  ds(2of(kx))?Void ds(2of(kx))?Void
Def == kl:Knd IdLnk fp-> (tg:Id IdLnk fp-> (tg:Id
Def == kl:Knd IdLnk fp-> ( IdLnk fp-> ( State(ds) State(ds)  ma-valtype(da; 1of(kl)) ma-valtype(da; 1of(kl)) 
Def == kl:Knd IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List
Def ==  x:Id fp-> Knd List x:Id fp-> Knd List ltg:IdLnk ltg:IdLnk Id fp-> Knd List Id fp-> Knd List Top Top |
| | | Thm* MsgA  Type{i'} Type{i'} |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| ma-state | Def State(ds) == x:Id  ds(x)?Top ds(x)?Top |
|
| ma-valtype | Def ma-valtype(da; k) == da(k)?Top |
|
| Id | Def Id == Atom 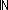 |
| | | Thm* Id  Type Type |
|
| ma-single-effect1 | Def ma-single-effect1(x;A;y;B;k;T;f)
Def == ma-single-effect(x : A 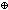 y : B; k : T; k; x; ( y : B; k : T; k; x; (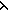 s,v. f(s(x),s(y),v))) s,v. f(s(x),s(y),v))) |
|
| fpf-join | Def f 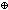 g == <1of(f) @ filter( g == <1of(f) @ filter(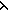 a. a.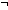 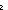 a a  dom(f);1of(g)), dom(f);1of(g)),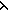 a.f(a)?g(a)> a.f(a)?g(a)> |
|
| fpf-cap | Def f(x)?z == if x  dom(f) dom(f)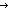 f(x) else z fi f(x) else z fi |
|
| fpf-single | Def x : v == <[x],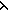 x.v> x.v> |
|
| id-deq | Def IdDeq == product-deq(Atom;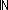 ;AtomDeq;NatDeq) ;AtomDeq;NatDeq) |
|
| not | Def 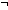 A == A A == A 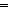 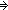 False False |
| | | Thm*  A:Prop. ( A:Prop. (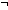 A) A)  Prop Prop |