is mentioned by

Thm* i,a,x:Id, A,T:Type, P:(ATProp). Thm* @i: ma-single-pre1(x;A;a;T;x,v.P(x,v))  Dsys Thm* & (D:Dsys.  Thm* & (@i: ma-single-pre1(x;A;a;T;x,v.P(x,v))  D Thm* & ( Thm* & (D  Thm* & (realizes es.(vartype(i;x) r A) Thm* & (realizes es.& (e:E.  Thm* & (realizes es.& (loc(e) = i  Id Thm* & (realizes es.& ( Thm* & (realizes es.& (kind(e) = locl(a)  Knd  (valtype(e) r T)) Thm* & (realizes es.& (e:E.  Thm* & (realizes es.& (loc(e) = i  Id Thm* & (realizes es.& ( Thm* & (realizes es.& ((kind(e) = locl(a)  Knd  P((x when e),val(e))) Thm* & (realizes es.& (& (e':E.  Thm* & (realizes es.& (& ((e <loc e')  e = e'  E Thm* & (realizes es.& (& (& kind(e') = locl(a)  Knd Thm* & (realizes es.& (& (&  (v:T. P((x after e'),v)))))	[s-pre-rule1]
Thm* i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds)TProp). Thm* @i: (with ds: ds action a:T precondition a(v) is P s v)  Dsys Thm* & (D:Dsys.  Thm* & (@i: (with ds: ds Thm* & (@action a:T Thm* & (@precondition a(v) is Thm* & (@P s v)  D Thm* & ( Thm* & (D  Thm* & (realizes es.(x:Id. vartype(i;x) r ds(x)?Top) Thm* & (realizes es.& (e:E.  Thm* & (realizes es.& (loc(e) = i  Id Thm* & (realizes es.& ( Thm* & (realizes es.& (kind(e) = locl(a)  Knd  (valtype(e) r T)) Thm* & (realizes es.& (e:E.  Thm* & (realizes es.& (loc(e) = i  Id Thm* & (realizes es.& ( Thm* & (realizes es.& ((kind(e) = locl(a)  Knd  P((z.(z when e)),val(e))) Thm* & (realizes es.& (& (e':E.  Thm* & (realizes es.& (& ((e <loc e')  e = e'  E Thm* & (realizes es.& (& (& kind(e') = locl(a)  Knd Thm* & (realizes es.& (& (&  (v:T. P((z.(z after e')),v)))))	[s-pre-rule]
Thm* i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds)TProp), Thm* init:x:Id fp-> ds(x)?Void. Thm* (x:Id. x  dom(ds)  x  dom(init)) Thm*  Thm* @i: (with ds: ds init: initaction a:T precondition a(v) is P)  Dsys Thm* & (D:Dsys.  Thm* & (@i: (with ds: ds Thm* & (@init: init Thm* & (action a:T Thm* & (aprecondition a(v) is Thm* & (aP)  D Thm* & ( Thm* & (D  Thm* & (realizes es.(v:T. P((x.init(x)?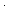),v))  (e:E. loc(e) = i  Id))	[s-pre-init-rule]
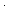Thm* i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)TProp), Thm* init:x:Id fp-> ds(x)?Void. Thm* (x:Id. x  dom(ds)  x  dom(init)) Thm*  Thm* @i (with ds: ds Thm* @i init: init Thm* @i action a:T Thm* @i precondition a(v) is Thm* @i P s v)  Thm* realizes es.(v:T. P((x.init(x)?),v))  (e:E. loc(e) = i  Id)	[pre-init-rule]
Thm* i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)TProp). Thm* @i (with ds: ds Thm* @i action a:T Thm* @i precondition a(v) is Thm* @i P s v)  Thm* realizes es.(x:Id. vartype(i;x) r ds(x)?Top) Thm* realizes es.& (e:E.  Thm* realizes es.& (loc(e) = i  Id Thm* realizes es.& ( Thm* realizes es.& (kind(e) = locl(a)  Knd  (valtype(e) r T)) Thm* realizes es.& (e:E.  Thm* realizes es.& (loc(e) = i  Id Thm* realizes es.& ( Thm* realizes es.& ((kind(e) = locl(a)  Knd  P((z.(z when e)),val(e))) Thm* realizes es.& (& (e':E.  Thm* realizes es.& (& ((e <loc e')  e = e'  E Thm* realizes es.& (& (& kind(e') = locl(a)  Knd Thm* realizes es.& (& (&  (v:T. P((z.(z after e')),v))))	[pre-rule]
Thm* D,D':Dsys, P:({es:ES| es is an event system of D }Prop{i'}). Thm* D realizes es.P(es)  D  D'  D' realizes es.P(es)	[realizes-monotone-wrt-sub]
Thm* D:Dsys, P:({es:ES| es is an event system of D }Prop{i'}). Thm* D realizes2 es.P(es)  D realizes es.P(es)	[d-realizes2-implies-realizes]
Thm* D:Dsys, P:({es:ES| es is an event system of D }Prop{i'}). Thm* D realizes2 es.P(es)  Prop{i''}	[d-realizes2_wf]
Thm* D:Dsys, P:({es:ES| es is an event system of D }Prop{i'}). Thm* D realizes es.P(es)  Prop{i''}	[d-realizes_wf]
Thm* D:Dsys, w:World. PossibleWorld(D;w)  Prop{i'}	[possible-world_wf]
Thm* A:Dsys, i,a:Id. a declared in M(i)  Prop	[ma-decla_wf2]
Thm* D1,D2:Dsys. D1  D2  Prop{i'}	[d-sub_wf]
Thm* a:Id, T,A:Type, x:Id, P:(ATProp). Thm* T Thm*  Thm* A Thm*  Thm* (a:A. Dec(v:T. P(a,v)))  Feasible(ma-single-pre1(x;A;a;T;x,v.P(x,v)))	[ma-single-pre1-feasible]
Thm* a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)TProp). Thm* T Thm*  Thm* xdom(ds). A=ds(x)   A Thm*  Thm* (s:State(ds). Dec(v:T. P(s,v))) Thm*  Thm* Feasible((with ds: ds Thm* Faction a:T Thm* Fprecondition a(v) is Thm* FP s v))	[ma-single-pre-feasible]
Thm* x:Id, c:T, a:Id, P:(TT'Prop). Thm* T' Thm*  Thm* (u:T. Dec(v:T'. P(u,v))) Thm*  Thm* Feasible(ma-single-pre-init1(x;T;c;a;T';x,v.P(x,v)))	[ma-single-pre-init1-feasible]
Thm* L:MsgA List, P:(IdLnkIdTypeProp), i:Id. Thm* (ML.(ltgma-outlinks(M;i).P(ltg)))  (ltgma-outlinks((L);i).P(ltg))	[ma-outlinks-join-list]
Thm* A,B:MsgA. ma-sframe-compatible(A; B)  Prop	[ma-sframe-compatible_wf]
Thm* A,B:MsgA. ma-frame-compatible(A; B)  Prop	[ma-frame-compatible_wf]
Thm* M:MsgA. Feasible(M)  Prop{i'}	[ma-feasible_wf]
Thm* T,T':Type, x:Id, c:T, a:Id, P:(TT'Prop). Thm* ma-single-pre-init1(x;T;c;a;T';x,v.P(x,v))  MsgA	[ma-single-pre-init1_wf]
Thm* a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)TProp), Thm* init:x:Id fp-> ds(x)?Void. Thm* (with ds: ds init: initaction a:T precondition a(v) is P)  MsgA	[ma-single-pre-init_wf]
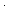Thm* P:(UnitProp). Dec(P())  Dec(x:Unit. P(x))	[decidable__ex_unit]
Thm* P:(TProp). (x:T. Dec(P(x)))  finite-type(T)  Dec(x:T. P(x))	[decidable-exists-finite]

In prior sections: core fun 1 well fnd int 1 bool 1 int 2 list 1 mb basic rel 1 mb nat mb list 1 mb list 2 mb event system 1 mb event system 2 mb event system 3 mb event system 4 mb event system 5

Try larger context: EventSystems IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html