Selected Objects
| def | d-es |
es is an event system of D
==  w:World, p:FairFifo. PossibleWorld(D;w) & es = ES(w) w:World, p:FairFifo. PossibleWorld(D;w) & es = ES(w)  ES ES |
| def | d-realizes |
D
realizes es.P(es)
==  D':Dsys. D D':Dsys. D  D' D'   ( ( w:World, p:FairFifo. PossibleWorld(D';w) w:World, p:FairFifo. PossibleWorld(D';w)   P(ES(w))) P(ES(w))) |
| def | d-realizes2 |
D realizes2 es.P(es) ==  w:World, p:FairFifo. PossibleWorld(D;w) w:World, p:FairFifo. PossibleWorld(D;w)   P(ES(w)) P(ES(w)) |
| def | msystem |
System == {M:(Id  MsgA)| MsgA)|  loc:Id. Feasible(M(loc)) } loc:Id. Feasible(M(loc)) } |
| def | m-sys-at |
@i: A(j) == if j = i A else fi A else fi |
| THM | s-at-sub-s-at |
 i:Id, A,B:MsgA. @i: A i:Id, A,B:MsgA. @i: A  @i: B @i: B 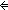  A A  B B |
| THM | bool-inhabited |
 |
| THM | decidable-exists-finite |
 P:(T P:(T  Prop). ( Prop). ( x:T. Dec(P(x))) x:T. Dec(P(x)))   finite-type(T) finite-type(T)   Dec( Dec( x:T. P(x)) x:T. P(x)) |
| THM | decidable__ex_unit |
 P:(Unit P:(Unit  Prop). Dec(P( Prop). Dec(P(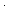 )) ))   Dec( Dec( x:Unit. P(x)) x:Unit. P(x)) |
| THM | ma-empty-frame-compatible-left |
 A:MsgA. ma-frame-compatible(; A) A:MsgA. ma-frame-compatible(; A) |
| THM | ma-empty-sframe-compatible-right |
 A:MsgA. ma-sframe-compatible(A; ) A:MsgA. ma-sframe-compatible(A; ) |
| THM | ma-empty-frame-compatible-right |
 A:MsgA. ma-frame-compatible(A; ) A:MsgA. ma-frame-compatible(A; ) |
| THM | ma-empty-sframe-compatible-left |
 A:MsgA. ma-sframe-compatible(; A) A:MsgA. ma-sframe-compatible(; A) |
| THM | ma-compatible-join |
 A,B,C:MsgA. A,B,C:MsgA.
A || B
 
ma-frame-compatible(A; B)
 
ma-sframe-compatible(A; B)
 
C || A
 
ma-frame-compatible(C; A)
 
ma-sframe-compatible(C; A)
 
C || B
 
ma-frame-compatible(C; B)
 
ma-sframe-compatible(C; B)
 
C || A  B & ma-frame-compatible(C; A B & ma-frame-compatible(C; A  B) & ma-sframe-compatible(C; A B) & ma-sframe-compatible(C; A  B) B) |
| THM | ma-compat-symmetry |
 A,B:MsgA. A ||+ B A,B:MsgA. A ||+ B   B ||+ A B ||+ A |
| THM | ma-empty-compat-left |
 A:MsgA. ||+ A A:MsgA. ||+ A |
| THM | ma-empty-compat-right |
 A:MsgA. A ||+ A:MsgA. A ||+ |
| THM | ma-join-feasible |
 A,B:MsgA. A,B:MsgA.
A || B
 
ma-frame-compatible(A; B)
 
ma-sframe-compatible(A; B)   Feasible(A) Feasible(A)   Feasible(B) Feasible(B)   Feasible(A Feasible(A  B) B) |
| THM | ma-compat-join |
 A,B,C:MsgA. A ||+ B A,B,C:MsgA. A ||+ B   C ||+ A C ||+ A   C ||+ B C ||+ B   C ||+ A C ||+ A  B B |
| THM | ma-join-list-property |
 L:MsgA List. L:MsgA List.
( A,B A,B L.A ||+ B) L.A ||+ B)    (L) (L)  MsgA & ( MsgA & ( M:MsgA. ( M:MsgA. ( B B L.M ||+ B) L.M ||+ B)   M ||+ M ||+  (L)) (L)) |
| THM | ma-sub-join-list |
 L:MsgA List, M:MsgA. ( L:MsgA List, M:MsgA. ( A,B A,B L.A ||+ B) L.A ||+ B)   (M (M  L) L)   M M   (L) (L) |
| THM | ma-join-list-feasible |
 L:MsgA List. ( L:MsgA List. ( A,B A,B L.A ||+ B) L.A ||+ B)   ( ( A A L.Feasible(A)) L.Feasible(A))   Feasible( Feasible( (L)) (L)) |
| THM | ma-join-list-compat |
 L:MsgA List. ( L:MsgA List. ( A,B A,B L.A ||+ B) L.A ||+ B)   ( ( M:MsgA. ( M:MsgA. ( B B L.M ||+ B) L.M ||+ B)   M ||+ M ||+  (L)) (L)) |
| THM | ma-join-list-compat2 |
 L:MsgA List. ( L:MsgA List. ( A,B A,B L.A ||+ B) L.A ||+ B)   ( ( M:MsgA. ( M:MsgA. ( B B L.B ||+ M) L.B ||+ M)    (L) ||+ M) (L) ||+ M) |
| THM | msga-sub-msg-form |
MsgA  r MsgAForm r MsgAForm |
| THM | msg-form-join |
 A,B:MsgAForm. A A,B:MsgAForm. A  B B  MsgAForm MsgAForm |
| THM | msg-form-join-list |
 L:MsgA List. L:MsgA List.  (L) (L)  MsgAForm MsgAForm |
| THM | ma-join-list-is-empty |
 L:MsgA List. ma-is-empty( L:MsgA List. ma-is-empty( (L)) ~ reduce( (L)) ~ reduce( M,x. ma-is-empty(M) M,x. ma-is-empty(M)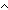  x;true x;true ;L) ;L) |
| THM | assert-ma-join-list-is-empty |
 L:MsgA List. ma-is-empty( L:MsgA List. ma-is-empty( (L)) (L)) 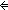  reduce( reduce( M,x. ma-is-empty(M) & x;True;L) M,x. ma-is-empty(M) & x;True;L) |
| THM | ma-outlinks-join |
 A,B:MsgAForm, ltg:(IdLnk A,B:MsgAForm, ltg:(IdLnk Id Id Type), i:Id. Type), i:Id.
(ltg  ma-outlinks(A ma-outlinks(A  B;i)) B;i))
 
(ltg  ma-outlinks(A;i)) ma-outlinks(A;i))  (ltg (ltg  ma-outlinks(B;i)) ma-outlinks(B;i)) |
| THM | ma-outlinks-join-list |
 L:MsgA List, P:(IdLnk L:MsgA List, P:(IdLnk Id Id Type Type  Prop), i:Id. Prop), i:Id.
( M M L.( L.( ltg ltg ma-outlinks(M;i).P(ltg))) ma-outlinks(M;i).P(ltg)))   ( ( ltg ltg ma-outlinks( ma-outlinks( (L);i).P(ltg)) (L);i).P(ltg)) |
| THM | sub-join-list-din |
 l:IdLnk, tg:Id, L:MsgA List. ( l:IdLnk, tg:Id, L:MsgA List. ( M M L.T L.T  r M.din(l,tg)) r M.din(l,tg))   (T (T  r r  (L).din(l,tg)) (L).din(l,tg)) |
| THM | ma-single-pre-init1-feasible |
 x:Id, c:T, a:Id, P:(T x:Id, c:T, a:Id, P:(T  T' T'  Prop). Prop).
T'
 
( u:T. Dec( u:T. Dec( v:T'. P(u,v))) v:T'. P(u,v)))
 
Feasible(ma-single-pre-init1(x;T;c;a;T';x,v.P(x,v))) |
| THM | ma-single-effect-feasible |
 x:Id, k:Knd, ds:x:Id fp-> Type, da:a:Knd fp-> Type, x:Id, k:Knd, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
 f:(State(ds) f:(State(ds)  ma-valtype(da; k) ma-valtype(da; k)  ds(x)?Void). ds(x)?Void).
 x x dom(ds). A=ds(x) dom(ds). A=ds(x)   A A
 
 k k dom(da). A=da(k) dom(da). A=da(k)   A A   Feasible(ma-single-effect(ds; da; k; x; f)) Feasible(ma-single-effect(ds; da; k; x; f)) |
| THM | ma-single-effect0-feasible |
 x:Id, k:Knd, A,T:Type, f:(A x:Id, k:Knd, A,T:Type, f:(A  T T  A). A).
A   T T   Feasible(ma-single-effect0(x;A;k;T;f)) Feasible(ma-single-effect0(x;A;k;T;f)) |
| THM | ma-single-pre-feasible |
 a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds) a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)  T T  Prop). Prop).
T
 
 x x dom(ds). A=ds(x) dom(ds). A=ds(x)   A A
 
( s:State(ds). Dec( s:State(ds). Dec( v:T. P(s,v))) v:T. P(s,v)))
 
Feasible((with ds: ds
Faction a:T
Fprecondition a(v) is
FP s v)) |
| THM | ma-single-pre1-feasible |
 a:Id, T,A:Type, x:Id, P:(A a:Id, T,A:Type, x:Id, P:(A  T T  Prop). Prop).
T
 
A   ( ( a:A. Dec( a:A. Dec( v:T. P(a,v))) v:T. P(a,v)))   Feasible(ma-single-pre1(x;A;a;T;x,v.P(x,v))) Feasible(ma-single-pre1(x;A;a;T;x,v.P(x,v))) |
| THM | ma-single-sends-feasible |
 k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
 f:(tg:Id f:(tg:Id State(ds) State(ds)  ma-valtype(da; k) ma-valtype(da; k)  (da(rcv(l; tg))?Void List)) List. (da(rcv(l; tg))?Void List)) List.
 x x dom(ds). A=ds(x) dom(ds). A=ds(x)   A A
 
 k k dom(da). A=da(k) dom(da). A=da(k)   A A   Feasible(ma-single-sends(ds; da; k; l; f)) Feasible(ma-single-sends(ds; da; k; l; f)) |
| THM | d-sub_transitivity |
 D1,D2,D3:Dsys. D1 D1,D2,D3:Dsys. D1  D2 D2   D2 D2  D3 D3   D1 D1  D3 D3 |
| THM | decidable__ma-decla |
 A:Dsys, i,a:Id. Dec(a declared in M(i)) A:Dsys, i,a:Id. Dec(a declared in M(i)) |
| THM | finite-support-feasible |
 D:Dsys, L:Id List. D:Dsys, L:Id List.
( i:Id. (i i:Id. (i  L) L)  ma-is-empty(M(i))) ma-is-empty(M(i)))
 
( i:Id. Feasible(M(i))) i:Id. Feasible(M(i)))
 
( i i L.( L.( ltg ltg ma-outlinks(M(i);i).(destination(1of(ltg)) ma-outlinks(M(i);i).(destination(1of(ltg))  L) L)
( i i L.( L.( ltg ltg ma-outlinks(M(i);i). ma-outlinks(M(i);i). 
interface-check(D;1of(ltg);1of(2of(ltg));2of(2of(ltg)))))
 
d-feasible(D) |
| THM | possible-world-monotonic |
 A,B:Dsys. A A,B:Dsys. A  B B   ( ( w:World. PossibleWorld(B;w) w:World. PossibleWorld(B;w)   PossibleWorld(A;w)) PossibleWorld(A;w)) |
| THM | d-realizes2-implies-realizes |
 D:Dsys, P:({es:ES| es is an event system of D } D:Dsys, P:({es:ES| es is an event system of D }  Prop{i'}). Prop{i'}).
D realizes2 es.P(es)   D realizes es.P(es) D realizes es.P(es) |
| THM | realizes-monotone-wrt-sub |
 D,D':Dsys, P:({es:ES| es is an event system of D } D,D':Dsys, P:({es:ES| es is an event system of D }  Prop{i'}). Prop{i'}).
D realizes es.P(es)   D D  D' D'   D' realizes es.P(es) D' realizes es.P(es) |
| THM | init-rule |
 i:Id, T:Type, v:T, x:Id. i:Id, T:Type, v:T, x:Id.
@i: x:T
@i: xinitially x = v
realizes es.(vartype(i;x)  r T) r T)
realizes es.& ( e:E. loc(e) = i e:E. loc(e) = i  Id Id   first(e) first(e)   (x when e) = v (x when e) = v  T) T) |
| THM | frame-rule |
 i:Id, L:Knd List, x:Id, T:Type. i:Id, L:Knd List, x:Id, T:Type.
@i: only L affects x : T
realizes es.(vartype(i;x)  r T) r T)
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id
realizes es.& ( 
realizes es.& (( (x after e) = (x when e) (x after e) = (x when e)  T T   (kind(e) (kind(e)  L)) L))
realizes es.& (& ( (kind(e) (kind(e)  L) L)   (x after e) = (x when e) (x after e) = (x when e)  T)) T)) |
| THM | sframe-rule |
 i:Id, L:Knd List, l:IdLnk, tg:Id. i:Id, L:Knd List, l:IdLnk, tg:Id.
@i: only L sends on (l with tg)
realizes es. e:E. loc(e) = i e:E. loc(e) = i  Id Id    null(sends(l,tg,e)) null(sends(l,tg,e))   (kind(e) (kind(e)  L) L) |
| THM | effect-rule |
 i,x:Id, k:Knd, ds:x:Id fp-> Type, da:a:Knd fp-> Type, i,x:Id, k:Knd, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
 f:(State(ds) f:(State(ds)  ma-valtype(da; k) ma-valtype(da; k)  ds(x)?Void). ds(x)?Void).
d-single-effect(i; ds; da; k; x; f)
realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
realizes es.& ( e:E. loc(e) = i e:E. loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id
realizes es.& ( 
realizes es.& (kind(e) = k  Knd Knd
realizes es.& ( 
realizes es.& ((x after e) = f(( z.(z when e)),val(e)) z.(z when e)),val(e))  ds(x)?Top) ds(x)?Top) |
| THM | sends-rule |
 i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type, i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
 f:(tg:Id f:(tg:Id State(ds) State(ds)  ma-valtype(da; k) ma-valtype(da; k)  (da(rcv(l; tg))?Void List)) List. (da(rcv(l; tg))?Void List)) List.
source(l) = i
 
d-single-sends(i; ds; da; k; l; f)
realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
realizes es.& ( e:E. loc(e) = i e:E. loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
realizes es.& ( e:E. e:E.
realizes es.& (isrcv(e)
realizes es.& ( 
realizes es.& (lnk(e) = l  IdLnk IdLnk   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
realizes es.& ({m:Msg| source(mlnk(m)) = i }  r Msg r Msg
realizes es.& ((( l,tg. da(rcv(l; tg))?Top))) l,tg. da(rcv(l; tg))?Top)))
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id
realizes es.& ( 
realizes es.& (kind(e) = k  Knd Knd
realizes es.& ( 
realizes es.& (sends(l;e)
realizes es.& (=
realizes es.& (tagged-messages(l; z.(z when e);val(e);f) z.(z when e);val(e);f)
realizes es.& ( Msg(( Msg(( l,tg. da(rcv(l; tg))?Top)) List) l,tg. da(rcv(l; tg))?Top)) List) |
| THM | better-sends-rule |
 i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type, i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
 f:(tg:Id f:(tg:Id State(ds) State(ds)  ma-valtype(da; k) ma-valtype(da; k)  (da(rcv(l; tg))?Void List)) List. (da(rcv(l; tg))?Void List)) List.
source(l) = i
 
d-single-sends(i; ds; da; k; l; f)
realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
realizes es.& ( e:E. loc(e) = i e:E. loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
realizes es.& ( e:E. e:E.
realizes es.& (isrcv(e)
realizes es.& ( 
realizes es.& (lnk(e) = l  IdLnk IdLnk   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id
realizes es.& ( 
realizes es.& (kind(e) = k  Knd Knd
realizes es.& ( 
realizes es.& (( L:{e':E| isrcv(e') & lnk(e') = l L:{e':E| isrcv(e') & lnk(e') = l  IdLnk } List. IdLnk } List.
realizes es.& ((( e':E. e':E.
realizes es.& ((((e'  L) L)
realizes es.& (((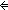 
realizes es.& (((isrcv(e') & lnk(e') = l  IdLnk & sender(e') = e IdLnk & sender(e') = e  E) E)
realizes es.& ((& ( e1,e2:E. e1 before e2 e1,e2:E. e1 before e2  L L   (e1 <loc e2)) (e1 <loc e2))
realizes es.& ((& map( e'.<tag(e'),val(e')>;L) e'.<tag(e'),val(e')>;L)
realizes es.& ((& =
realizes es.& ((& tagged-list-messages( z.(z when e);val(e);f) z.(z when e);val(e);f)
realizes es.& ((&  (tg:Id (tg:Id ma-valtype(da; rcv(l; tg))) List)) ma-valtype(da; rcv(l; tg))) List)) |
| THM | pre-rule |
 i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds) i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)  T T  Prop). Prop).
@i (with ds: ds
@i action a:T
@i precondition a(v) is
@i P s v)
realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id   kind(e) = locl(a) kind(e) = locl(a)  Knd Knd   (valtype(e) (valtype(e)  r T)) r T))
realizes es.& ( e:E. e:E.
realizes es.& (loc(e) = i  Id Id
realizes es.& ( 
realizes es.& ((kind(e) = locl(a)  Knd Knd   P(( P(( z.(z when e)),val(e))) z.(z when e)),val(e)))
realizes es.& (& ( e':E. e':E.
realizes es.& (& ((e <loc e')  e = e' e = e'  E E
realizes es.& (& (& kind(e') = locl(a)  Knd Knd  ( ( v:T. v:T.  P(( P(( z.(z after e')),v)))) z.(z after e')),v)))) |
| THM | pre-init-rule |
 i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds) i,a:Id, T:Type, ds:x:Id fp-> Type, P:(State(ds)  T T  Prop), Prop),
 init:x:Id fp-> ds(x)?Void. init:x:Id fp-> ds(x)?Void.
( x:Id. x x:Id. x  dom(ds) dom(ds)   x x  dom(init)) dom(init))
 
@i (with ds: ds
@i init: init
@i action a:T
@i precondition a(v) is
@i P s v)
realizes es.( v:T. P(( v:T. P(( x.init(x)? x.init(x)?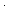 ),v)) ),v))   ( ( e:E. loc(e) = i e:E. loc(e) = i  Id) Id) |
| THM | s-pre-init-rule |
 i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds) i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds)  T T  Prop), Prop),
 init:x:Id fp-> ds(x)?Void. init:x:Id fp-> ds(x)?Void.
( x:Id. x x:Id. x  dom(ds) dom(ds)   x x  dom(init)) dom(init))
 
@i: (with ds: ds init: initaction a:T precondition a(v) is P)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: (with ds: ds
& (@init: init
& (action a:T
& (aprecondition a(v) is
& (aP)  D D
& ( 
& (D
& (realizes es.( v:T. P(( v:T. P(( x.init(x)? x.init(x)?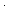 ),v)) ),v))   ( ( e:E. loc(e) = i e:E. loc(e) = i  Id)) Id)) |
| THM | s-pre-rule |
 i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds) i,a:Id, T:Type, ds:a:Id fp-> Type, P:(State(ds)  T T  Prop). Prop).
@i: (with ds: ds action a:T precondition a(v) is P s v)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: (with ds: ds
& (@action a:T
& (@precondition a(v) is
& (@P s v)  D D
& ( 
& (D
& (realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = locl(a)  Knd Knd   (valtype(e) (valtype(e)  r T)) r T))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& ((kind(e) = locl(a)  Knd Knd   P(( P(( z.(z when e)),val(e))) z.(z when e)),val(e)))
& (realizes es.& (& ( e':E. e':E.
& (realizes es.& (& ((e <loc e')  e = e' e = e'  E E
& (realizes es.& (& (& kind(e') = locl(a)  Knd Knd
& (realizes es.& (& (&  ( ( v:T. v:T.  P(( P(( z.(z after e')),v))))) z.(z after e')),v))))) |
| THM | s-pre-rule1 |
 i,a,x:Id, A,T:Type, P:(A i,a,x:Id, A,T:Type, P:(A  T T  Prop). Prop).
@i: ma-single-pre1(x;A;a;T;x,v.P(x,v))  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: ma-single-pre1(x;A;a;T;x,v.P(x,v))  D D
& ( 
& (D
& (realizes es.(vartype(i;x)  r A) r A)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = locl(a)  Knd Knd   (valtype(e) (valtype(e)  r T)) r T))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& ((kind(e) = locl(a)  Knd Knd   P((x when e),val(e))) P((x when e),val(e)))
& (realizes es.& (& ( e':E. e':E.
& (realizes es.& (& ((e <loc e')  e = e' e = e'  E E
& (realizes es.& (& (& kind(e') = locl(a)  Knd Knd  ( ( v:T. v:T.  P((x after e'),v))))) P((x after e'),v))))) |
| THM | s-effect-rule |
 i,x:Id, k:Knd, ds:a:Id fp-> Type, da:a:Knd fp-> Type, i,x:Id, k:Knd, ds:a:Id fp-> Type, da:a:Knd fp-> Type,
 f:(State(ds) f:(State(ds)  ma-valtype(da; k) ma-valtype(da; k)  ds(x)?Void). ds(x)?Void).
@i: ma-single-effect(ds; da; k; x; f)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: ma-single-effect(ds; da; k; x; f)  D D
& ( 
& (D
& (realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = k  Knd Knd
& (realizes es.& ( 
& (realizes es.& ((x after e) = f(( z.(z when e)),val(e)) z.(z when e)),val(e))  ds(x)?Top)) ds(x)?Top)) |
| THM | s-effect-rule0 |
 i,x:Id, a:Knd, T,A:Type, f:(A i,x:Id, a:Knd, T,A:Type, f:(A  T T  A). A).
@i: ma-single-effect0(x;A;a;T;f)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: ma-single-effect0(x;A;a;T;f)  D D
& ( 
& (D
& (realizes es.(vartype(i;x)  r A) r A)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id   kind(e) = a kind(e) = a  Knd Knd   (valtype(e) (valtype(e)  r T)) r T))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = a  Knd Knd   (x after e) = f((x when e),val(e)) (x after e) = f((x when e),val(e))  A)) A)) |
| THM | effect-rule1 |
 i,x,y:Id, k:Knd, T,A,B:Type, f:(A i,x,y:Id, k:Knd, T,A,B:Type, f:(A  B B  T T  A). A).
 y = x y = x
 
@i: ma-single-effect1(x;A;y;B;k;T;f)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: ma-single-effect1(x;A;y;B;k;T;f)  D D
& ( 
& (D
& (realizes es.(vartype(i;x)  r A) & (vartype(i;y) r A) & (vartype(i;y)  r B) r B)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id   kind(e) = k kind(e) = k  Knd Knd   (valtype(e) (valtype(e)  r T)) r T))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = k  Knd Knd
& (realizes es.& ( 
& (realizes es.& ((x after e) = f((x when e),(y when e),val(e))  A)) A)) |
| THM | s-sends-rule |
 i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:k:Knd fp-> Type, i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:k:Knd fp-> Type,
 f:(tg:Id f:(tg:Id State(ds) State(ds)  ma-valtype(da; k) ma-valtype(da; k)  (da(rcv(l; tg))?Void List)) List. (da(rcv(l; tg))?Void List)) List.
source(l) = i
 
@i: ma-single-sends(ds; da; k; l; f)  Dsys Dsys
& ( D:Dsys. D:Dsys.
& (@i: ma-single-sends(ds; da; k; l; f)  D D
& ( 
& (D
& (realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (isrcv(e)
& (realizes es.& ( 
& (realizes es.& (lnk(e) = l  IdLnk IdLnk   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
& (realizes es.& ( e:E. e:E.
& (realizes es.& (loc(e) = i  Id Id
& (realizes es.& ( 
& (realizes es.& (kind(e) = k  Knd Knd
& (realizes es.& ( 
& (realizes es.& (( L:{e':E| isrcv(e') & lnk(e') = l L:{e':E| isrcv(e') & lnk(e') = l  IdLnk } List. IdLnk } List.
& (realizes es.& ((( e':E. e':E.
& (realizes es.& ((((e'  L) L)
& (realizes es.& (((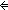 
& (realizes es.& (((isrcv(e') & lnk(e') = l  IdLnk & sender(e') = e IdLnk & sender(e') = e  E) E)
& (realizes es.& ((& ( e1,e2:E. e1 before e2 e1,e2:E. e1 before e2  L L   (e1 <loc e2)) (e1 <loc e2))
& (realizes es.& ((& map( e'.<tag(e'),val(e')>;L) e'.<tag(e'),val(e')>;L)
& (realizes es.& ((& =
& (realizes es.& ((& tagged-list-messages( z.(z when e);val(e);f) z.(z when e);val(e);f)
& (realizes es.& ((&  (tg:Id (tg:Id ma-valtype(da; rcv(l; tg))) List))) ma-valtype(da; rcv(l; tg))) List))) |