| | Who Cites d-es? |
|
| d-es | Def es is an event system of D
Def ==  w:World, p:FairFifo. PossibleWorld(D;w) & es = ES(w) w:World, p:FairFifo. PossibleWorld(D;w) & es = ES(w)  ES ES |
|
| w-es | Def ES(the_w;p)
Def == <E
Def == ,product-deq(Id; ;IdDeq;NatDeq) ;IdDeq;NatDeq)
Def == ,( i,x. vartype(i;x)) i,x. vartype(i;x))
Def == ,( i,a. V(i;locl(a))) i,a. V(i;locl(a)))
Def == ,the_w.M
Def == ,
Def == ,( e.loc(e)) e.loc(e))
Def == ,( e.kind(e)) e.kind(e))
Def == ,( e.val(e)) e.val(e))
Def == ,( x,e. (x when e)) x,e. (x when e))
Def == ,( x,e. (x after e)) x,e. (x after e))
Def == ,( l,e. sends(l;e)) l,e. sends(l;e))
Def == ,( e.sender(e)) e.sender(e))
Def == ,( e.index(e)) e.index(e))
Def == ,( e.first(e)) e.first(e))
Def == ,( e.pred(e)) e.pred(e))
Def == ,( e,e'. e <c e') e,e'. e <c e')
Def == ,world_DASH_event_DASH_system{1:l, i:l}(the_w,p)
Def == , > > |
|
| event_system | Def ES
Def == E:Type
Def ==  EqDecider(E) EqDecider(E) (T:Id (T:Id  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( V:Id V:Id  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top (loc:E (loc:E  Id Id
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( kind:E kind:E  Knd Knd
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( val:(e:E val:(e:E  eventtype(kind;loc;V;M;e)) eventtype(kind;loc;V;M;e))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( when:(x:Id when:(x:Id  e:E e:E  T(loc(e),x)) T(loc(e),x))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( after:(x:Id after:(x:Id  e:E e:E  T(loc(e),x)) T(loc(e),x))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( sends:(l:IdLnk sends:(l:IdLnk  E E  (Msg_sub(l; M) List)) (Msg_sub(l; M) List))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( sender:{e:E| sender:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }  E E
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||sends ||sends
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||(lnk(kind(e)) ||(lnk(kind(e))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||,sender(e))||) ||,sender(e))||)
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( first:E first:E  
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( pred:{e':E| pred:{e':E|   (first(e')) } (first(e')) }  E E
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( causl:E causl:E  E E  Prop Prop
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms{i:l} ESAxioms{i:l}
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(E; ESAxioms(E;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(T; ESAxioms(T;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(M; ESAxioms(M;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(loc; ESAxioms(loc;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(kind; ESAxioms(kind;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(val; ESAxioms(val;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(when; ESAxioms(when;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(after; ESAxioms(after;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(sends; ESAxioms(sends;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(sender; ESAxioms(sender;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(index; ESAxioms(index;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(first; ESAxioms(first;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(pred; ESAxioms(pred;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(causl) ESAxioms(causl)
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( Top)) Top)) |
| | | Thm* ES  Type{i'} Type{i'} |
|
| possible-world | Def PossibleWorld(D;w)
Def == FairFifo
Def == & ( i,x:Id. vartype(i;x) i,x:Id. vartype(i;x)  r M(i).ds(x)) r M(i).ds(x))
Def == & & ( i:Id, a:Action(i). i:Id, a:Action(i).
Def == & & (  isnull(a) isnull(a)   (valtype(i;a) (valtype(i;a)  r M(i).da(kind(a)))) r M(i).da(kind(a))))
Def == & & ( l:IdLnk, tg:Id. (w.M(l,tg)) l:IdLnk, tg:Id. (w.M(l,tg))  r M(source(l)).da(rcv(l; tg))) r M(source(l)).da(rcv(l; tg)))
Def == & & ( i,x:Id. M(i).init(x,s(i;0).x)) i,x:Id. M(i).init(x,s(i;0).x))
Def == & & ( i:Id, t: i:Id, t: . .
Def == & & (  isnull(a(i;t)) isnull(a(i;t))
Def == & & ( 
Def == & & (( islocal(kind(a(i;t))) islocal(kind(a(i;t)))
Def == & & (( 
Def == & & ((M(i).pre(act(kind(a(i;t))), x.s(i;t).x,val(a(i;t)))) x.s(i;t).x,val(a(i;t))))
Def == & & (& ( x:Id. x:Id.
Def == & & (& (M(i).ef(kind(a(i;t)),x, x.s(i;t).x,val(a(i;t)),s(i;t+1).x)) x.s(i;t).x,val(a(i;t)),s(i;t+1).x))
Def == & & (& ( l:IdLnk. l:IdLnk.
Def == & & (& (M(i).send(kind(a(i;t));l; x. x.
Def == & & (& (s(i;t).x;val(a(i;t));withlnk(l;m(i;t));i))
Def == & & (& ( x:Id. x:Id.
Def == & & (& ( M(i).frame(kind(a(i;t)) affects x) M(i).frame(kind(a(i;t)) affects x)
Def == & & (& ( 
Def == & & (& (s(i;t).x = s(i;t+1).x  M(i).ds(x)) M(i).ds(x))
Def == & & (& ( l:IdLnk, tg:Id. l:IdLnk, tg:Id.
Def == & & (& ( M(i).sframe(kind(a(i;t)) sends <l,tg>) M(i).sframe(kind(a(i;t)) sends <l,tg>)
Def == & & (& ( 
Def == & & (& (w-tagged(tg; onlnk(l;m(i;t))) = nil  Msg List)) Msg List))
Def == & & ( i,a:Id, t: i,a:Id, t: . .
Def == & & ( t': t': . .
Def == & & (t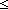 t' t'
Def == & & (&   isnull(a(i;t')) & kind(a(i;t')) = locl(a) isnull(a(i;t')) & kind(a(i;t')) = locl(a)
Def == & & (&   a declared in M(i) a declared in M(i)
Def == & & (&  unsolvable M(i).pre(a, unsolvable M(i).pre(a, x.s(i;t').x)) x.s(i;t').x)) |
|
| fair-fifo | Def FairFifo
Def == ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.  source(l) = i source(l) = i   onlnk(l;m(i;t)) = nil onlnk(l;m(i;t)) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: . .
Def == & ( isnull(a(i;t)) isnull(a(i;t))
Def == & ( 
Def == & (( x:Id. s(i;t+1).x = s(i;t).x x:Id. s(i;t+1).x = s(i;t).x  vartype(i;x)) vartype(i;x))
Def == & (& m(i;t) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.
Def == & ( isrcv(l;a(i;t)) isrcv(l;a(i;t))
Def == & ( 
Def == & (destination(l) = i
Def == & (& ||queue(l;t)||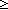 1 & hd(queue(l;t)) = msg(a(i;t)) 1 & hd(queue(l;t)) = msg(a(i;t))  Msg) Msg)
Def == & ( l:IdLnk, t: l:IdLnk, t: . .
Def == & ( t': t': . .
Def == & (t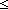 t' & t' &  isrcv(l;a(destination(l);t')) isrcv(l;a(destination(l);t'))  queue(l;t') = nil queue(l;t') = nil  Msg List) Msg List) |
|
| world | Def World
Def == T:Id  Id Id  Type Type
Def ==  TA:Id TA:Id  Id Id  Type Type
Def ==  M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
Def == (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| | | Thm* World  Type{i'} Type{i'} |
|
| w-causl | Def e <c e' == e  e,e'. e <loc e' e,e'. e <loc e'   isrcv(kind(e')) & e = sender(e') isrcv(kind(e')) & e = sender(e')  E^+ e' E^+ e' |
|
| w-pred | Def pred(e)
Def == if isnull(a(loc(e);time(e)-1)) pred(<loc(e),time(e)-1>) pred(<loc(e),time(e)-1>)
Def == else <loc(e),time(e)-1> fi
Def (recursive) |
|
| w-first | Def first(e)
Def == if time(e)= 0 0 true true
Def == i; isnull(a(loc(e);time(e)-1)) first(<loc(e),time(e)-1>) first(<loc(e),time(e)-1>)
Def == else false fi fi
Def (recursive) |
|
| w-index | Def index(e)
Def == ||rcvs(lnk(kind(e));time(e))||-||snds(lnk(kind(e));time(sender(e)))|| |
|
| w-sender | Def sender(e) == <source(lnk(kind(e))),mu( t.match(lnk(kind(e));t;time(e)))> t.match(lnk(kind(e));t;time(e)))> |
|
| w-sends | Def sends(l;e) == onlnk(l;m(loc(e);time(e))) |
|
| w-after | Def (x after e) == s(1of(e);2of(e)+1).x |
|
| w-when | Def (x when e) == s(1of(e);2of(e)).x |
|
| w-eval | Def val(e) == val(act(e)) |
|
| w-ekind | Def kind(e) == kind(act(e)) |
|
| w-locl | Def e <loc e' == loc(e) = loc(e')  Id & time(e)<time(e') Id & time(e)<time(e') |
|
| w-loc | Def loc(e) == 1of(e) |
|
| w-Msg | Def Msg == Msg(w.M) |
|
| w-valtype | Def valtype(i;a) == kindcase(kind(a);a.w.TA(i,a);l,tg.w.M(l,tg)) |
|
| w-action | Def Action(i) == action(w-action-dec(w.TA;w.M;i)) |
|
| w-M | Def w.M == 1of(2of(2of(w))) |
|
| ma-npre | Def unsolvable M.pre(a,s)
Def == P != 1of(2of(2of(2of(M))))(a) ==>  v:M.da(locl(a)). v:M.da(locl(a)).  P(s,v) P(s,v) |
|
| ma-decla | Def a declared in M ==  locl(a) locl(a)  dom(1of(2of(M))) dom(1of(2of(M))) |
|
| locl | Def locl(a) == inr(a) |
| | | Thm*  a:Id. locl(a) a:Id. locl(a)  Knd Knd |
|
| w-V | Def V(i;k) == kindcase(k;a.1of(2of(w))(i,a);l,tg.1of(2of(2of(w)))(l,tg)) |
|
| w-vartype | Def vartype(i;x) == w.T(i,x) |
|
| w-queue | Def queue(l;t) == nth_tl(||rcvs(l;t)||;snds(l;t)) |
|
| w-match | Def match(l;t;t')
Def == (||snds(l;t)||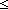  ||rcvs(l;t')||) ||rcvs(l;t')||)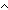 
Def == (||rcvs(l;t')||< ||snds(l;t)||+||onlnk(l;m(source(l);t))||) ||snds(l;t)||+||onlnk(l;m(source(l);t))||) |
|
| w-snds | Def snds(l;t) == concat(map( t1.m(l;t1);upto(t))) t1.m(l;t1);upto(t))) |
|
| w-ml | Def m(l;t) == onlnk(l;m(source(l);t)) |
|
| w-onlnk | Def onlnk(l;mss) == filter( ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
|
| w-tagged | Def w-tagged(tg; mss) == filter( ms.mtag(ms) = tg;mss) ms.mtag(ms) = tg;mss) |
|
| ma-sframe | Def M.sframe(k sends <l,tg>)
Def == L != 1of(2of(2of(2of(2of(2of(2of(2of(
Def == L != 1of(M))))))))(<l,tg>) ==>  deq-member(KindDeq;k;L) deq-member(KindDeq;k;L) |
|
| ma-ef | Def M.ef(k,x,s,v,w)
Def == E != 1of(2of(2of(2of(2of(M)))))(<k,x>) ==> w = E(s,v)  M.ds(x) M.ds(x) |
|
| ma-ds | Def M.ds(x) == 1of(M)(x)?Top |
|
| ma-frame | Def M.frame(k affects x)
Def == L != 1of(2of(2of(2of(2of(2of(2of(M)))))))(x) ==>  deq-member(KindDeq;k;L) deq-member(KindDeq;k;L) |
|
| w-withlnk | Def withlnk(l;mss) == mapfilter( ms.2of(ms); ms.2of(ms); ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
|
| ma-send | Def M.send(k;l;s;v;ms;i)
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> ms
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> =
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if source(l) = i
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if concat(map( tgf. tgf.
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if map( x. x.
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;2of(tgf)
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;(s
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;,v));L))
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> else nil fi
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  (tg:Id (tg:Id
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( if source(l) = i if source(l) = i
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( if M.da(rcv(l; tg)) if M.da(rcv(l; tg))
Def == L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( else Top fi) List else Top fi) List |
|
| ma-pre | Def M.pre(a,s,v) == P != 1of(2of(2of(2of(M))))(a) ==> P(s,v) |
|
| ma-init | Def M.init(x,v) == x0 != 1of(2of(2of(M)))(x) ==> v = x0  1of(M)(x)?Void 1of(M)(x)?Void |
|
| ma-da | Def M.da(a) == 1of(2of(M))(a)?Top |
|
| w-rcvs | Def rcvs(l;t) == filter( a.isrcv(l;a);map( a.isrcv(l;a);map( t1.a(destination(l);t1);upto(t))) t1.a(destination(l);t1);upto(t))) |
|
| w-isrcvl | Def isrcv(l;a) ==   isnull(a) isnull(a)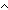  isrcv(kind(a)) isrcv(kind(a))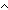  lnk(kind(a)) = l lnk(kind(a)) = l |
|
| w-action-dec | Def w-action-dec(TA;M;i)(k)
Def == kindcase(k;a.TA(i,a);l,tg.if destination(l) = i M(l,tg) else Void fi) M(l,tg) else Void fi) |
|
| Kind-deq | Def KindDeq == union-deq(IdLnk Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) |
|
| eq_lnk | Def a = b == eqof(IdLnkDeq)(a,b) |
| | | Thm*  a,b:IdLnk. a = b a,b:IdLnk. a = b   |
|
| eq_id | Def a = b == eqof(IdDeq)(a,b) |
| | | Thm*  a,b:Id. a = b a,b:Id. a = b   |
|
| idlnk-deq | Def IdLnkDeq == product-deq(Id;Id  ;IdDeq;product-deq(Id; ;IdDeq;product-deq(Id; ;IdDeq;NatDeq)) ;IdDeq;NatDeq)) |
|
| id-deq | Def IdDeq == product-deq(Atom; ;AtomDeq;NatDeq) ;AtomDeq;NatDeq) |
|
| nat-deq | Def NatDeq == < a,b. a= a,b. a= b,nat_DASH_deq_DASH_aux{1:l}> b,nat_DASH_deq_DASH_aux{1:l}> |
|
| w-E | Def E == {p:(Id  )| )|   isnull(a(1of(p);2of(p))) } isnull(a(1of(p);2of(p))) } |
|
| ESAxioms | Def ESAxioms{i:l}
Def ESAxioms(E;
Def ESAxioms(T;
Def ESAxioms(M;
Def ESAxioms(loc;
Def ESAxioms(kind;
Def ESAxioms(val;
Def ESAxioms(when;
Def ESAxioms(after;
Def ESAxioms(sends;
Def ESAxioms(sender;
Def ESAxioms(index;
Def ESAxioms(first;
Def ESAxioms(pred;
Def ESAxioms(causl)
Def == ( e,e':E. loc(e) = loc(e') e,e':E. loc(e) = loc(e')  Id Id   causl(e,e') causl(e,e')  e = e' e = e'  causl(e',e)) causl(e',e))
Def == & ( e:E. e:E.  (first(e)) (first(e)) 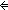  ( ( e':E. loc(e') = loc(e) e':E. loc(e') = loc(e)  Id Id    causl(e',e))) causl(e',e)))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))
Def == & ( 
Def == & (loc(pred(e)) = loc(e)  Id & causl(pred(e),e) Id & causl(pred(e),e)
Def == & (& ( e':E. e':E.
Def == & (& (loc(e') = loc(e)  Id Id    (causl(pred(e),e') & causl(e',e)))) (causl(pred(e),e') & causl(e',e))))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))   ( ( x:Id. when(x,e) = after(x,pred(e)) x:Id. when(x,e) = after(x,pred(e))  T(loc(e),x))) T(loc(e),x)))
Def == & (Trans e,e':E. causl(e,e'))
Def == & SWellFounded(causl(e,e'))
Def == & ( e:E. e:E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ((sends(lnk(kind(e)),sender(e)))[(index(e))]
Def == & (=
Def == & (msg(lnk(kind(e));tag(kind(e));val(e))
Def == & ( Msg(M)) Msg(M))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   causl(sender(e),e)) causl(sender(e),e))
Def == & ( e,e':E. e,e':E.
Def == & (causl(e,e')
Def == & ( 
Def == & (  (first(e')) & causl(e,pred(e')) (first(e')) & causl(e,pred(e'))  e = pred(e') e = pred(e')
Def == & (  isrcv(kind(e')) & causl(e,sender(e')) isrcv(kind(e')) & causl(e,sender(e'))  e = sender(e')) e = sender(e'))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   loc(e) = destination(lnk(kind(e)))) loc(e) = destination(lnk(kind(e))))
Def == & ( e:E, l:IdLnk. e:E, l:IdLnk.
Def == & ( loc(e) = source(l) loc(e) = source(l)   sends(l,e) = nil sends(l,e) = nil  Msg_sub(l; M) List) Msg_sub(l; M) List)
Def == & ( e,e':E. e,e':E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ( isrcv(kind(e')) isrcv(kind(e'))
Def == & ( 
Def == & (lnk(kind(e)) = lnk(kind(e'))
Def == & ( 
Def == & ((causl(e,e')
Def == & ((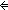 
Def == & ((causl(sender(e),sender(e'))
Def == & (( sender(e) = sender(e') sender(e) = sender(e')  E & index(e)<index(e'))) E & index(e)<index(e')))
Def == & ( e:E, l:IdLnk, n: e:E, l:IdLnk, n: ||sends(l,e)||. ||sends(l,e)||.
Def == & ( e':E. e':E.
Def == & ( isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) |
| | | Thm*  E:Type{i}, T,V:(Id E:Type{i}, T,V:(Id  Id Id  Type{i}), M:(IdLnk Type{i}), M:(IdLnk  Id Id  Type{i}), loc:(E Type{i}), loc:(E  Id), Id),
Thm*  kind:(E kind:(E  Knd), val:(e:E Knd), val:(e:E  eventtype(kind;loc;V;M;e)), eventtype(kind;loc;V;M;e)),
Thm*  when,after:(x:Id when,after:(x:Id  e:E e:E  T(loc(e),x)), T(loc(e),x)),
Thm*  sends:(l:IdLnk sends:(l:IdLnk  E E  (Msg_sub(l; M) List)), (Msg_sub(l; M) List)),
Thm*  sender:({e:E| isrcv(kind(e)) } sender:({e:E| isrcv(kind(e)) }  E), E),
Thm*  index:(e:{e:E| isrcv(kind(e)) } index:(e:{e:E| isrcv(kind(e)) }   ||sends(lnk(kind(e)),sender(e))||), ||sends(lnk(kind(e)),sender(e))||),
Thm*  first:(E first:(E   ), pred:({e':E| ), pred:({e':E|  first(e') } first(e') }  E), causl:(E E), causl:(E  E E  Prop{i}). Prop{i}).
Thm* ESAxioms{i:l}
Thm* ESAxioms(E;
Thm* ESAxioms(T;
Thm* ESAxioms(M;
Thm* ESAxioms(loc;
Thm* ESAxioms(kind;
Thm* ESAxioms(val;
Thm* ESAxioms(when;
Thm* ESAxioms(after;
Thm* ESAxioms(sends;
Thm* ESAxioms(sender;
Thm* ESAxioms(index;
Thm* ESAxioms(first;
Thm* ESAxioms(pred;
Thm* ESAxioms(causl)
Thm*  Prop{i'} Prop{i'} |
|
| Msg_sub | Def Msg_sub(l; M) == {m:Msg(M)| haslink(l; m) } |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), l:IdLnk. Msg_sub(l; M) Type), l:IdLnk. Msg_sub(l; M)  Type Type |
|
| action | Def action(dec) == Unit+(k:Knd dec(k)) dec(k)) |
| | | Thm*  dec:(Knd dec:(Knd  Type). action(dec) Type). action(dec)  Type Type |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| Msg | Def Msg(M) == l:IdLnk t:Id t:Id M(l,t) M(l,t) |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type). Msg(M) Type). Msg(M)  Type Type |
|
| haslink | Def haslink(l; m) == mlnk(m) = l |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), l:IdLnk, m:Msg(M). haslink(l; m) Type), l:IdLnk, m:Msg(M). haslink(l; m)  Prop Prop |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| strongwellfounded | Def SWellFounded(R(x;y)) ==  f:(T f:(T   ). ).  x,y:T. R(x;y) x,y:T. R(x;y)   f(x)<f(y) f(x)<f(y) |
| | | Thm*  T:Type, R:(T T:Type, R:(T  T T  Type). SWellFounded(R(x,y)) Type). SWellFounded(R(x,y))  Prop Prop |
|
| nat | Def  == {i: == {i: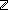 | 0 | 0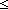 i } i } |
| | | Thm*   Type Type |
|
| product-deq | Def product-deq(A;B;a;b) == <proddeq(a;b),prod-deq(A;B;a;b)> |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |
|
| deq | Def EqDecider(T) == eq:T  T T     x,y:T. x = y x,y:T. x = y 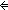   (eq(x,y)) (eq(x,y)) |
| | | Thm*  T:Type. EqDecider(T) T:Type. EqDecider(T)  Type Type |
|
| prod-deq | Def prod-deq(A;B;a;b)
Def == ( A,B,a,b,p,q. q/q1,q2. A,B,a,b,p,q. q/q1,q2.
Def == (p/p1,p2.
Def == (b/eq,b1.
Def == (a/e1,a1.
Def == (( %1.%1 %1.%1
Def == (( %1.(< %1.(< %.<( %.<( %1.%1(p1,q1)/%4,%5. %4(( %1.%1(p1,q1)/%4,%5. %4(( %1.%1)(( %1.%1)(( %1.*)(*))))(a1) %1.*)(*))))(a1)
Def == (( %1.(< %1.(< %.,( %.,( %1.%1(p2,q2)/%4,%5. %4(( %1.%1(p2,q2)/%4,%5. %4(( %1.%1)(( %1.%1)(( %1.*)(*))))(b1)> %1.*)(*))))(b1)>
Def == (( %1.(, %1.(, %.%/%1,%2. *>)) %.%/%1,%2. *>))
Def == ((( %1.%1.2) %1.%1.2)
Def == (((( %1.%1 %1.%1
Def == (((( %1.(<p1,p2> = <q1,q2> %1.(<p1,p2> = <q1,q2>  A A B B
Def == (((( %1.,<p1,p2> = <q1,q2> %1.,<p1,p2> = <q1,q2>  A A B B
Def == (((( %1., %1., ((e1(p1,q1)) ((e1(p1,q1))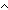  (eq(p2,q2))) (eq(p2,q2)))
Def == (((( %1., %1., (e1(p1,q1)) & (e1(p1,q1)) &  (eq(p2,q2)) (eq(p2,q2))
Def == (((( %1.,( %1.,( %1.%1)(( %1.%1)(( %1.< %1.< %2.%2, %2.%2, %2.%2>)(*)) %2.%2>)(*))
Def == (((( %1.,( %1.,( %1.%1) %1.%1)
Def == (((( %1.,(( %1.,(( %1.%1(e1(p1,q1),eq(p2,q2))) %1.%1(e1(p1,q1),eq(p2,q2)))
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase(p p,q. InjCase(q; x. InjCase(p
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; x. < p,q. InjCase(q; x. InjCase; x. < %.<*,*>, %.<*,*>, %.*> %.*>
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; y. < p,q. InjCase(q; x. InjCase; y. < %.<any(%),*> %.<any(%),*>
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; y. , p,q. InjCase(q; x. InjCase; y. , %.%/%1,%2. any(%1)>) %.%/%1,%2. any(%1)>)
Def == (((( %1.,(( %1.,(( p,q. ; y. p,q. ; y.
Def == (((( %1.,(( %1.,(( p,q. InjCase(p p,q. InjCase(p
Def == (((( %1.,(( %1.,(( p,q. InjCase; x. < p,q. InjCase; x. < %.<*,any(%)>, %.<*,any(%)>, %.%/%1,%2. any(%2)> %.%/%1,%2. any(%2)>
Def == (((( %1.,(( %1.,(( p,q. InjCase; y. < p,q. InjCase; y. < %.<any(%),any(%)> %.<any(%),any(%)>
Def == (((( %1.,(( %1.,(( p,q. InjCase; y. , p,q. InjCase; y. , %.%/%1,%2. any(%2)>)))))) %.%/%1,%2. any(%2)>))))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(%5 %3.(%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((%5 %3.((((%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((((%6(( %3.(((((((%6(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((((%)))) %3.(((((((%))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(%1) %3.(%1)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(%5 %3.(%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((%6 %3.((((%6
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((((%6(( %3.(((((((%6(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((((%1)))) %3.(((((((%1))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(%)> %3.(%)>
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(%6 %3.(%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((%5 %3.((((%5
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((((%5(( %3.(((((((%5(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((((%)))) %3.(((((((%))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(%1) %3.(%1)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(%6 %3.(%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((%6 %3.((((%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((((%5(( %3.(((((((%5(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((((%1)))) %3.(((((((%1))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(%)>>)))) %3.(%)>>))))
Def == (A
Def == ,B
Def == ,a
Def == ,b) |
|
| fpf-val | Def z != f(x) ==> P(a;z) ==  x x  dom(f) dom(f)   P(x;f(x)) P(x;f(x)) |
|
| assert | Def  b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: . b . b  Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: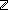 | i | i 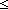 k < j } k < j } |
| | | Thm*  m,n: m,n: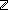 . {m..n . {m..n } }  Type Type |
|
| ge | Def i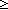 j == j j == j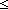 i i |
| | | Thm*  i,j: i,j: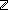 . (i . (i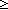 j) j)  Prop Prop |
|
| lelt | Def i 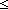 j < k == i j < k == i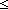 j & j<k j & j<k |
|
| le | Def A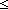 B == B ==  B<A B<A |
| | | Thm*  i,j: i,j: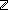 . (i . (i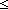 j) j)  Prop Prop |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| eventtype | Def eventtype(k;loc;V;M;e) == kindcase(k(e);a.V(loc(e),a);l,t.M(l,t)) |
| | | Thm*  E:Type, V:(Id E:Type, V:(Id  Id Id  Type), M:(IdLnk Type), M:(IdLnk  Id Id  Type), loc:(E Type), loc:(E  Id), k:(E Id), k:(E  Knd), Knd),
Thm*  e:E. eventtype(k;loc;V;M;e) e:E. eventtype(k;loc;V;M;e)  Type Type |
|
| w-msg | Def msg(a) == msg(lnk(kind(a));tag(kind(a));val(a)) |
|
| kindcase | Def kindcase(k;a.f(a);l,t.g(l;t))
Def == if islocal(k) f(act(k)) else g(lnk(k);tag(k)) fi f(act(k)) else g(lnk(k);tag(k)) fi |
| | | Thm*  B:Type, k:Knd, f:(Id B:Type, k:Knd, f:(Id  B), g:(IdLnk B), g:(IdLnk  Id Id  B). B).
Thm* kindcase(k;a.f(a);l,t.g(l,t))  B B |
|
| lnk | Def lnk(k) == 1of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   lnk(k) lnk(k)  IdLnk IdLnk |
|
| length | Def ||as|| == Case of as; nil  0 ; a.as' 0 ; a.as'  ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||  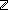 |
| | | Thm* ||nil||  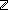 |
|
| isrcv | Def isrcv(k) == isl(k) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   |
|
| w-s | Def s(i;t).x == 1of(2of(2of(2of(w))))(i,t,x) |
|
| d-m | Def M(i) == D(i) |
|
| w-act | Def act(e) == a(1of(e);2of(e)) |
|
| w-a | Def a(i;t) == 1of(2of(2of(2of(2of(w)))))(i,t) |
|
| w-kind | Def kind(a) == 1of(outr(a)) |
|
| w-isnull | Def isnull(a) == isl(a) |
|
| w-m | Def m(i;t) == 1of(2of(2of(2of(2of(2of(w))))))(i,t) |
|
| w-val | Def val(a) == 2of(outr(a)) |
|
| actof | Def act(k) == outr(k) |
| | | Thm*  k:Knd. islocal(k) k:Knd. islocal(k)   act(k) act(k)  Id Id |
|
| islocal | Def islocal(k) ==   isl(k) isl(k) |
| | | Thm*  k:Knd. islocal(k) k:Knd. islocal(k)   |
|
| rcv | Def rcv(l; tg) == inl(<l,tg>) |
| | | Thm*  l:IdLnk, tg:Id. rcv(l; tg) l:IdLnk, tg:Id. rcv(l; tg)  Knd Knd |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| ldst | Def destination(l) == 1of(2of(l)) |
| | | Thm*  l:IdLnk. destination(l) l:IdLnk. destination(l)  Id Id |
|
| select | Def l[i] == hd(nth_tl(i;l)) |
| | | Thm*  A:Type, l:A List, n: A:Type, l:A List, n: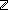 . 0 . 0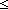 n n   n<||l|| n<||l||   l[n] l[n]  A A |
|
| hd | Def hd(l) == Case of l; nil  "?" ; h.t "?" ; h.t  h h |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||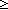 1 1   hd(l) hd(l)  A A |
|
| mlnk | Def mlnk(m) == 1of(m) |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), m:Msg(M). mlnk(m) Type), m:Msg(M). mlnk(m)  IdLnk IdLnk |
| | | Thm*  the_es:ES, m:Msg. mlnk(m) the_es:ES, m:Msg. mlnk(m)  IdLnk IdLnk |
|
| rel_plus | Def R^+(x,y) ==  n: n: 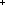 . x R^n y . x R^n y |
| | | Thm*  T:Type, R:(T T:Type, R:(T  T T  Type). R^+ Type). R^+  T T  T T  Type Type |
|
| w-time | Def time(e) == 2of(e) |
|
| rel_exp | Def R^n == if n= 0 0  x,y. x = y x,y. x = y  T else T else  x,y. x,y.  z:T. (x R z) & (z R^n-1 y) fi z:T. (x R z) & (z R^n-1 y) fi
Def (recursive) |
| | | Thm*  n: n: , T:Type, R:(T , T:Type, R:(T  T T  Prop). R^n Prop). R^n  T T  T T  Prop Prop |
|
| upto | Def upto(n) == if n= 0 0 nil else upto(n-1) @ [(n-1)] fi (recursive) nil else upto(n-1) @ [(n-1)] fi (recursive) |
| | | Thm*  n: n: . upto(n) . upto(n)   n List n List |
|
| eq_int | Def i= j == if i=j j == if i=j true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: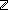 . (i= . (i= j) j)   |
|
| mu | Def mu(f) == if f(0) 0 else mu( 0 else mu( x.f(x+1))+1 fi (recursive) x.f(x+1))+1 fi (recursive) |
| | | Thm*  f:( f:(    ). ( ). ( n: n: . f(n)) . f(n))   mu(f) mu(f)   |
|
| proddeq | Def proddeq(a;b)(p,q) == (1of(a)(1of(p),1of(q)))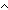  (1of(b)(2of(p),2of(q))) (1of(b)(2of(p),2of(q))) |
| | | Thm*  A,B:Type, a:EqDecider(A), b:EqDecider(B). proddeq(a;b) A,B:Type, a:EqDecider(A), b:EqDecider(B). proddeq(a;b)  A A B B  A A B B   |
|
| tagof | Def tag(k) == 2of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   tag(k) tag(k)  Id Id |
|
| mtag | Def mtag(m) == 1of(2of(m)) |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), m:Msg(M). mtag(m) Type), m:Msg(M). mtag(m)  Id Id |
|
| fpf-cap | Def f(x)?z == if x  dom(f) dom(f) f(x) else z fi f(x) else z fi |
|
| w-TA | Def w.TA == 1of(2of(w)) |
|
| fpf-ap | Def f(x) == 2of(f)(x) |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| w-T | Def w.T == 1of(w) |
|
| fpf-dom | Def x  dom(f) == deq-member(eq;x;1of(f)) dom(f) == deq-member(eq;x;1of(f)) |
|
| deq-member | Def deq-member(eq;x;L) == reduce( a,b. eqof(eq)(a,x) a,b. eqof(eq)(a,x)   b;false b;false ;L) ;L) |
|
| union-deq | Def union-deq(A;B;a;b) == <sumdeq(a;b),sum-deq(A;B;a;b)> |
|
| eqof | Def eqof(d) == 1of(d) |
| | | Thm*  T:Type, d:EqDecider(T). eqof(d) T:Type, d:EqDecider(T). eqof(d)  T T  T T   |
|
| sumdeq | Def sumdeq(a;b)(p,q)
Def == InjCase(p; pa. InjCase(q; qa. 1of(a)(pa,qa); qb. false ); pb. ); pb.
Def == InjCase(q; qa. false ; qb. 1of(b)(pb,qb))) ; qb. 1of(b)(pb,qb))) |
| | | Thm*  A,B:Type, a:EqDecider(A), b:EqDecider(B). sumdeq(a;b) A,B:Type, a:EqDecider(A), b:EqDecider(B). sumdeq(a;b)  (A+B) (A+B)  (A+B) (A+B)   |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| atom-deq | Def AtomDeq == < a,b. a= a,b. a= b b Atom,atom_DASH_deq_DASH_aux{1:l}> Atom,atom_DASH_deq_DASH_aux{1:l}> |
|
| iff | Def P 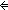  Q == (P Q == (P   Q) & (P Q) & (P 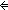  Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A 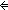  B) B)  Prop Prop |
|
| trans | Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (Trans x,y:T. E(x,y)) Prop). (Trans x,y:T. E(x,y))  Prop Prop |
|
| outl | Def outl(x) == InjCase(x; y. y; z. "???") |
| | | Thm*  A,B:Type, x:A+B. isl(x) A,B:Type, x:A+B. isl(x)   outl(x) outl(x)  A A |
|
| isl | Def isl(x) == InjCase(x; y. true ; z. false ; z. false ) ) |
| | | Thm*  A,B:Type, x:A+B. isl(x) A,B:Type, x:A+B. isl(x)   |
|
| outr | Def outr(x) == InjCase(x; y. "???"; z. z) |
| | | Thm*  A,B:Type, x:A+B. A,B:Type, x:A+B.   isl(x) isl(x)   outr(x) outr(x)  B B |
|
| mapfilter | Def mapfilter(f;P;L) == map(f;filter(P;L)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T   ), T':Type, f:({x:T| P(x) } ), T':Type, f:({x:T| P(x) }  T'), L:T List. T'), L:T List.
Thm* mapfilter(f;P;L)  T' List T' List |
|
| filter | Def filter(P;l) == reduce( a,v. if P(a) a,v. if P(a) [a / v] else v fi;nil;l) [a / v] else v fi;nil;l) |
| | | Thm*  T:Type, P:(T T:Type, P:(T   ), l:T List. filter(P;l) ), l:T List. filter(P;l)  T List T List |
|
| map | Def map(f;as) == Case of as; nil  nil ; a.as' nil ; a.as'  [(f(a)) / map(f;as')] [(f(a)) / map(f;as')]
Def (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List. map(f;l) B), l:A List. map(f;l)  B List B List |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List B), l:A List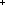 . map(f;l) . map(f;l)  B List B List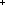 |
|
| concat | Def concat(ll) == reduce( l,l'. l @ l';nil;ll) l,l'. l @ l';nil;ll) |
| | | Thm*  T:Type, ll:(T List) List. concat(ll) T:Type, ll:(T List) List. concat(ll)  T List T List |
|
| nth_tl | Def nth_tl(n;as) == if n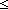  0 0 as else nth_tl(n-1;tl(as)) fi (recursive) as else nth_tl(n-1;tl(as)) fi (recursive) |
| | | Thm*  A:Type, as:A List, i: A:Type, as:A List, i: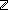 . nth_tl(i;as) . nth_tl(i;as)  A List A List |
|
| le_int | Def i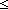  j == j ==   j< j< i i |
| | | Thm*  i,j: i,j: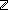 . (i . (i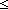  j) j)   |
|
| bnot | Def   b == if b b == if b false false else true else true fi fi |
| | | Thm*  b: b: . .   b b   |
|
| band | Def p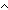  q == if p q == if p q else false q else false fi fi |
| | | Thm*  p,q: p,q: . (p . (p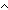  q) q)   |
|
| nat_plus | Def  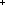 == {i: == {i: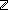 | 0<i } | 0<i } |
| | | Thm*  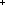  Type Type |
|
| lt_int | Def i< j == if i<j j == if i<j true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: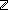 . (i< . (i< j) j)   |
|
| eq_atom | Def x= y y Atom == if x=y Atom == if x=y Atom Atom true true ; false ; false fi fi |
| | | Thm*  x,y:Atom. x= x,y:Atom. x= y y Atom Atom   |
|
| rev_implies | Def P 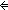  Q == Q Q == Q   P P |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A   B) B)  Prop Prop |
|
| reduce | Def reduce(f;k;as) == Case of as; nil  k ; a.as' k ; a.as'  f(a,reduce(f;k;as')) f(a,reduce(f;k;as'))
Def (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B B  B), k:B, as:A List. reduce(f;k;as) B), k:B, as:A List. reduce(f;k;as)  B B |
|
| bor | Def p   q == if p q == if p true true else q fi else q fi |
| | | Thm*  p,q: p,q: . (p . (p   q) q)   |
|
| append | Def as @ bs == Case of as; nil  bs ; a.as' bs ; a.as'  [a / (as' @ bs)] (recursive) [a / (as' @ bs)] (recursive) |
| | | Thm*  T:Type, as,bs:T List. (as @ bs) T:Type, as,bs:T List. (as @ bs)  T List T List |
|
| tl | Def tl(l) == Case of l; nil  nil ; h.t nil ; h.t  t t |
| | | Thm*  A:Type, l:A List. tl(l) A:Type, l:A List. tl(l)  A List A List |
|
| sum-deq | Def sum-deq(A;B;a;b)
Def == ( A,B,a,b,p,q. A,B,a,b,p,q.
Def == (InjCase(q; x. InjCase(p
Def == (InjCase(q; x. InjCase; x1. b/eq,b1.
Def == (InjCase(q; x. InjCase; x1. a/e1,a1.
Def == (InjCase(q; x. InjCase; x1. < %.( %.( %1.%1(x1,x)/%4,%5. %1.%1(x1,x)/%4,%5.
Def == (InjCase(q; x. InjCase; x1. < %.(%4 %.(%4
Def == (InjCase(q; x. InjCase; x1. < %.((( %.((( %1.%1) %1.%1)
Def == (InjCase(q; x. InjCase; x1. < %.(((( %.(((( %1.*) %1.*)
Def == (InjCase(q; x. InjCase; x1. < %.((((( %.((((( %1.%1(x)) %1.%1(x))
Def == (InjCase(q; x. InjCase; x1. < %.(((((( %.(((((( %1.%1(x1)) %1.%1(x1))
Def == (InjCase(q; x. InjCase; x1. < %.((((((( %.((((((( %1.%1(B)) %1.%1(B))
Def == (InjCase(q; x. InjCase; x1. < %.(((((((( %.(((((((( %1.%1(A)) %1.%1(A))
Def == (InjCase(q; x. InjCase; x1. < %.(((((((( %.(((((((( A,B,x1,x,%. ( A,B,x1,x,%. ( %1.%1) %1.%1)
Def == (InjCase(q; x. InjCase; x1. < %.(((((((( %.(((((((( A,B,x1,x,%. (( A,B,x1,x,%. (( %1.( %1.( %2.*)(*)) %2.*)(*))
Def == (InjCase(q; x. InjCase; x1. < %.(((((((( %.(((((((( A,B,x1,x,%. ((%)))))))))) A,B,x1,x,%. ((%))))))))))
Def == (InjCase(q; x. InjCase; x1. < %.(a1) %.(a1)
Def == (InjCase(q; x. InjCase; x1. , %.*> %.*>
Def == (InjCase(q; x. InjCase; y. b/eq,b1.
Def == (InjCase(q; x. InjCase; y. a/e1,a1.
Def == (InjCase(q; x. InjCase; y. < %.( %.( %1.any((%1(*)))) %1.any((%1(*))))
Def == (InjCase(q; x. InjCase; y. < %.(( %.(( %1.%1(x)) %1.%1(x))
Def == (InjCase(q; x. InjCase; y. < %.((( %.((( %1.%1(y)) %1.%1(y))
Def == (InjCase(q; x. InjCase; y. < %.(((( %.(((( %1.%1(B)) %1.%1(B))
Def == (InjCase(q; x. InjCase; y. < %.((((( %.((((( %1.%1(A)) %1.%1(A))
Def == (InjCase(q; x. InjCase; y. < %.((((( %.((((( A,B,y,x,%. A,B,y,x,%.
Def == (InjCase(q; x. InjCase; y. < %.(((((( %.(((((( %1. %1.
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase(%1 %.((((((InjCase(%1
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %2. any(%2) %.((((((InjCase; %2. any(%2)
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. ( %.((((((InjCase; %3. ( %4.any(%4)) %4.any(%4))
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. (( %.((((((InjCase; %3. (( %4.( %4.( %5.( %5.( %6. %6.
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. (( %.((((((InjCase; %3. (( %4.( %4.( %5.(any(%6)) %5.(any(%6))
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. (( %.((((((InjCase; %3. (( %4.( %4.( %5.(*)) %5.(*))
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. (( %.((((((InjCase; %3. (( %4.(*)) %4.(*))
Def == (InjCase(q; x. InjCase; y. < %.((((((InjCase; %3. ((%)))) %.((((((InjCase; %3. ((%))))
Def == (InjCase(q; x. InjCase; y. < %.((((((( %.((((((( %1.%1)(inr( %1.%1)(inr( %.*)))))))) %.*))))))))
Def == (InjCase(q; x. InjCase; y. , %.*>) %.*>)
Def == (; y.
Def == (InjCase(p
Def == (InjCase; x. b/eq,b1.
Def == (InjCase; x. a/e1,a1.
Def == (InjCase; x. < %.( %.( %1.any((%1(*)))) %1.any((%1(*))))
Def == (InjCase; x. < %.(( %.(( %1.%1(y)) %1.%1(y))
Def == (InjCase; x. < %.((( %.((( %1.%1(x)) %1.%1(x))
Def == (InjCase; x. < %.(((( %.(((( %1.%1(B)) %1.%1(B))
Def == (InjCase; x. < %.((((( %.((((( %1.%1(A)) %1.%1(A))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase(%1 %1.InjCase(%1
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %2. any(%2) %1.InjCase; %2. any(%2)
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. ( %1.InjCase; %3. ( %4.any(%4)) %4.any(%4))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. (( %1.InjCase; %3. (( %4.( %4.( %5.( %5.( %6. %6.
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. (( %1.InjCase; %3. (( %4.( %4.( %5.(any(%6)) %5.(any(%6))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. (( %1.InjCase; %3. (( %4.( %4.( %5.(*)) %5.(*))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. (( %1.InjCase; %3. (( %4.(*)) %4.(*))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. ( A,B,x,y,%. ( %1.InjCase; %3. ((%)))) %1.InjCase; %3. ((%))))
Def == (InjCase; x. < %.((((( %.((((( A,B,x,y,%. (( A,B,x,y,%. (( %1.%1)(inr( %1.%1)(inr( %.*)))))))) %.*))))))))
Def == (InjCase; x. , %.*> %.*>
Def == (InjCase; y1. b/eq,b1.
Def == (InjCase; y1. a/e1,a1.
Def == (InjCase; y1. < %.( %.( %1.%1(y1,y)/%4,%5. %1.%1(y1,y)/%4,%5.
Def == (InjCase; y1. < %.(%4 %.(%4
Def == (InjCase; y1. < %.((( %.((( %1.%1) %1.%1)
Def == (InjCase; y1. < %.(((( %.(((( %1.*) %1.*)
Def == (InjCase; y1. < %.((((( %.((((( %1.%1(y)) %1.%1(y))
Def == (InjCase; y1. < %.(((((( %.(((((( %1.%1(y1)) %1.%1(y1))
Def == (InjCase; y1. < %.((((((( %.((((((( %1.%1(B)) %1.%1(B))
Def == (InjCase; y1. < %.(((((((( %.(((((((( %1.%1(A)) %1.%1(A))
Def == (InjCase; y1. < %.(((((((( %.(((((((( A,B,y1,y,%. ( A,B,y1,y,%. ( %1.%1) %1.%1)
Def == (InjCase; y1. < %.(((((((( %.(((((((( A,B,y1,y,%. (( A,B,y1,y,%. (( %1.( %1.( %2.*)(*))(%)))))))))) %2.*)(*))(%))))))))))
Def == (InjCase; y1. < %.(b1) %.(b1)
Def == (InjCase; y1. , %.*>))) %.*>)))
Def == (A
Def == ,B
Def == ,a
Def == ,b) |