| prod-deq | Def prod-deq(A;B;a;b)
Def == ( A,B,a,b,p,q. q/q1,q2. A,B,a,b,p,q. q/q1,q2.
Def == (p/p1,p2.
Def == (b/eq,b1.
Def == (a/e1,a1.
Def == (( %1.%1 %1.%1
Def == (( %1.(< %1.(< %.<( %.<( %1.%1(p1,q1)/%4,%5. %4(( %1.%1(p1,q1)/%4,%5. %4(( %1.%1)(( %1.%1)(( %1.*)(*))))(a1) %1.*)(*))))(a1)
Def == (( %1.(< %1.(< %.,( %.,( %1.%1(p2,q2)/%4,%5. %4(( %1.%1(p2,q2)/%4,%5. %4(( %1.%1)(( %1.%1)(( %1.*)(*))))(b1)> %1.*)(*))))(b1)>
Def == (( %1.(, %1.(, %.%/%1,%2. *>)) %.%/%1,%2. *>))
Def == ((( %1.%1.2) %1.%1.2)
Def == (((( %1.%1 %1.%1
Def == (((( %1.(<p1,p2> = <q1,q2> %1.(<p1,p2> = <q1,q2>  A A B B
Def == (((( %1.,<p1,p2> = <q1,q2> %1.,<p1,p2> = <q1,q2>  A A B B
Def == (((( %1., %1., ((e1(p1,q1)) ((e1(p1,q1))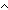  (eq(p2,q2))) (eq(p2,q2)))
Def == (((( %1., %1., (e1(p1,q1)) & (e1(p1,q1)) &  (eq(p2,q2)) (eq(p2,q2))
Def == (((( %1.,( %1.,( %1.%1)(( %1.%1)(( %1.< %1.< %2.%2, %2.%2, %2.%2>)(*)) %2.%2>)(*))
Def == (((( %1.,( %1.,( %1.%1) %1.%1)
Def == (((( %1.,(( %1.,(( %1.%1(e1(p1,q1),eq(p2,q2))) %1.%1(e1(p1,q1),eq(p2,q2)))
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase(p p,q. InjCase(q; x. InjCase(p
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; x. < p,q. InjCase(q; x. InjCase; x. < %.<*,*>, %.<*,*>, %.*> %.*>
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; y. < p,q. InjCase(q; x. InjCase; y. < %.<any(%),*> %.<any(%),*>
Def == (((( %1.,(( %1.,(( p,q. InjCase(q; x. InjCase; y. , p,q. InjCase(q; x. InjCase; y. , %.%/%1,%2. any(%1)>) %.%/%1,%2. any(%1)>)
Def == (((( %1.,(( %1.,(( p,q. ; y. p,q. ; y.
Def == (((( %1.,(( %1.,(( p,q. InjCase(p p,q. InjCase(p
Def == (((( %1.,(( %1.,(( p,q. InjCase; x. < p,q. InjCase; x. < %.<*,any(%)>, %.<*,any(%)>, %.%/%1,%2. any(%2)> %.%/%1,%2. any(%2)>
Def == (((( %1.,(( %1.,(( p,q. InjCase; y. < p,q. InjCase; y. < %.<any(%),any(%)> %.<any(%),any(%)>
Def == (((( %1.,(( %1.,(( p,q. InjCase; y. , p,q. InjCase; y. , %.%/%1,%2. any(%2)>)))))) %.%/%1,%2. any(%2)>))))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(%5 %3.(%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((%5 %3.((((%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((((%6(( %3.(((((((%6(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(((((((%)))) %3.(((((((%))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2.< %2.< %3.(%1) %3.(%1)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(%5 %3.(%5
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((%6 %3.((((%6
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((((%6(( %3.(((((((%6(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(((((((%1)))) %3.(((((((%1))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. < P1,P2,Q1,Q2,%,%1. < %2., %2., %3.(%)> %3.(%)>
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(%6 %3.(%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((%5 %3.((((%5
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((((%5(( %3.(((((((%5(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(((((((%)))) %3.(((((((%))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2.< %2.< %3.(%1) %3.(%1)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.( %3.( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(%6 %3.(%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((( %3.((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((( %3.(((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((%6 %3.((((%6
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((( %3.(((((( %4.%4) %4.%4)
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((((( %3.((((((( %4.%4/%5,%6. %4.%4/%5,%6.
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((((%5(( %3.(((((((%5(( %4.%4)(( %4.%4)(( %4.%4)(%3)))) %4.%4)(%3))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(((((((%1)))) %3.(((((((%1))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.((((%2)))) %3.((((%2))))
Def == (((( P1,P2,Q1,Q2,%,%1. , P1,P2,Q1,Q2,%,%1. , %2., %2., %3.(%)>>)))) %3.(%)>>))))
Def == (A
Def == ,B
Def == ,a
Def == ,b) |