| Rank | Theorem | Name |
| 6 | Thm*  A,B:MsgA. A,B:MsgA.
Thm* A || B
Thm*  
Thm* ma-frame-compatible(A; B)
Thm*  
Thm* ma-sframe-compatible(A; B)   Feasible(A) Feasible(A)   Feasible(B) Feasible(B)   Feasible(A Feasible(A  B) B) | [ma-join-feasible] |
| cites the following: |
| 3 | Thm*  B:(A B:(A  Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A. Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A.
Thm* x  dom(f dom(f  g) g) 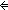  x x  dom(f) dom(f)  x x  dom(g) dom(g) | [fpf-join-dom] |
| 4 | Thm*  B:(A B:(A  Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A. Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A.
Thm* x  dom(f dom(f  g) g)   f f  g(x) = if x g(x) = if x  dom(f) dom(f) f(x) else g(x) fi f(x) else g(x) fi  B(x) B(x) | [fpf-join-ap] |
| 5 | Thm*  B:(A B:(A  Type), eq:EqDecider(A), f,g:a:A fp-> B(a). f || g Type), eq:EqDecider(A), f,g:a:A fp-> B(a). f || g   g g  f f  g g | [fpf-sub-join-right] |
| 5 | Thm*  B1,B2:(A B1,B2:(A  Type), eq:EqDecider(A), f:a:A fp-> B1(a), g:a:A fp-> B2(a). Type), eq:EqDecider(A), f:a:A fp-> B1(a), g:a:A fp-> B2(a).
Thm* f  f f  g g | [fpf-sub-join-left] |
| 0 | Thm*  eq:EqDecider(X), f,g:x:X fp-> Type. g eq:EqDecider(X), f,g:x:X fp-> Type. g  f f   ( ( x:X. f(x)?Top x:X. f(x)?Top  r g(x)?Top) r g(x)?Top) | [subtype-fpf-cap] |
| 4 | Thm*  eq:EqDecider(A), f,g:a:A fp-> Top, x:A, z:Top. eq:EqDecider(A), f,g:a:A fp-> Top, x:A, z:Top.
Thm* f  g(x)?z ~ if x g(x)?z ~ if x  dom(f) dom(f) f(x)?z else g(x)?z fi f(x)?z else g(x)?z fi | [fpf-join-cap-sq] |
| 0 | Thm*  eq:EqDecider(A), f:a:A fp-> Top, g:Top, x:A. eq:EqDecider(A), f:a:A fp-> Top, g:Top, x:A.
Thm* f  g(x) ~ if x g(x) ~ if x  dom(f) dom(f) f(x) else g(x) fi f(x) else g(x) fi | [fpf-join-ap-sq] |
| 4 | Thm*  eq:EqDecider(A), f,g:a:A fp-> Top, x:A. eq:EqDecider(A), f,g:a:A fp-> Top, x:A.
Thm* x  dom(f dom(f  g) g) 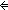  x x  dom(f) dom(f)  x x  dom(g) dom(g) | [fpf-join-dom2] |