| Rank | Theorem | Name |
| 5 | Thm*  i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type, i:Id, k:Knd, l:IdLnk, ds:x:Id fp-> Type, da:a:Knd fp-> Type,
Thm*  f:(tg:Id f:(tg:Id State(ds) State(ds)  ma-valtype(da; k) ma-valtype(da; k)  (da(rcv(l; tg))?Void List)) List. (da(rcv(l; tg))?Void List)) List.
Thm* source(l) = i
Thm*  
Thm* d-single-sends(i; ds; da; k; l; f)
Thm* realizes es.( x:Id. vartype(i;x) x:Id. vartype(i;x)  r ds(x)?Top) r ds(x)?Top)
Thm* realizes es.& ( e:E. e:E.
Thm* realizes es.& (loc(e) = i  Id Id   (valtype(e) (valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
Thm* realizes es.& ( e:E. e:E.
Thm* realizes es.& (isrcv(e)
Thm* realizes es.& ( 
Thm* realizes es.& (lnk(e) = l  IdLnk IdLnk
Thm* realizes es.& ( 
Thm* realizes es.& ((valtype(e)  r ma-valtype(da; kind(e)))) r ma-valtype(da; kind(e))))
Thm* realizes es.& ({m:Msg| source(mlnk(m)) = i }  r Msg r Msg
Thm* realizes es.& ((( l,tg. da(rcv(l; tg))?Top))) l,tg. da(rcv(l; tg))?Top)))
Thm* realizes es.& ( e:E. e:E.
Thm* realizes es.& (loc(e) = i  Id Id
Thm* realizes es.& ( 
Thm* realizes es.& (kind(e) = k  Knd Knd
Thm* realizes es.& ( 
Thm* realizes es.& (sends(l;e)
Thm* realizes es.& (=
Thm* realizes es.& (tagged-messages(l; z.(z when e);val(e);f) z.(z when e);val(e);f)
Thm* realizes es.& ( Msg(( Msg(( l,tg. da(rcv(l; tg))?Top)) List) l,tg. da(rcv(l; tg))?Top)) List) | [sends-rule] |
| cites the following: |
| 3 | Thm*  D:Dsys, P:({es:ES| es is an event system of D } D:Dsys, P:({es:ES| es is an event system of D }  Prop{i'}). Prop{i'}).
Thm* D realizes2 es.P(es)   D realizes es.P(es) D realizes es.P(es) | [d-realizes2-implies-realizes] |
| 0 | Thm*  the_w:World, e:E. act(e) the_w:World, e:E. act(e)  {a:Action(loc(e))| {a:Action(loc(e))|  isnull(a) } isnull(a) } | [w-act_wf] |
| 1 | Thm* strong-subtype(A;B)   (EqDecider(B) (EqDecider(B)  r EqDecider(A)) r EqDecider(A)) | [strong-subtype-deq-subtype] |
| 0 | Thm*  d:EqDecider(A), i:A. (eqof(d)(i,i)) ~ true d:EqDecider(A), i:A. (eqof(d)(i,i)) ~ true | [eqof_eq_btrue] |
| 1 | Thm*  i:Id, w:World, p:FairFifo, t: i:Id, w:World, p:FairFifo, t: . .
Thm*  isnull(a(i;t)) isnull(a(i;t))   (valtype(<i,t>) ~ valtype(i;a(i;t))) (valtype(<i,t>) ~ valtype(i;a(i;t))) | [es-valtype-w-valtype] |
| 0 | Thm*  as:Top List, f,g:Top. map(g;map(f;as)) ~ map(g o f;as) as:Top List, f,g:Top. map(g;map(f;as)) ~ map(g o f;as) | [map-map] |
| 0 | Thm*  T:Type, P:(T T:Type, P:(T   ), l:T List. filter(P;l) ), l:T List. filter(P;l)  {x:T| P(x) } List {x:T| P(x) } List | [filter_type] |
| 4 | Thm*  a:T List, f:(T a:T List, f:(T  T). ( T). ( x:T. (x x:T. (x  a) a)   f(x) = x) f(x) = x)   map(f;a) = a map(f;a) = a | [trivial_map] |
| 0 | Thm*  f:(A f:(A  B), l:A List. map(f;l) = nil B), l:A List. map(f;l) = nil 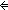  l = nil l = nil | [map_is_nil] |