Switchable Properties

Next: About this document ... Up: Proof of the Switch Previous: Proof of the Switch

Switchable Properties

Having proved that out switch preserves all switchable properties, we should show that some interesting properties are switchable. The ``smallest'' switchable property is Causal 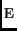No-dup-deliver

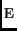
$\begin{program*} \>\mforall{}E:EventStruct. (switchable$_{\mbox{\small {E}}}$\ (... ...x{\small {E}}}$\ \mwedge{} No-dup-deliver$_{\mbox{\small {E}}}$)) \end{program*}$
This follows from the fact that both of the properties satisfy all six of the metaproperties in
$\begin{program*} \> \\ \> switchable0(E) P ==\\ \> safetyR$_{\mbox{\small {E}}... ...s P\\ \> \mwedge{} delayableR$_{\mbox{\small {E}}}$\ preserves P \end{program*}$
Any property P that satisfies these six meta-proerties can be conjoined with Causal 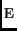No-dup-deliver 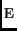to get a switchable property.
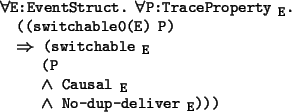
$\begin{program*} \> \\ \> \mforall{}E:EventStruct. \mforall{}P:TraceProperty$_{... ...ll {E}}}$\\ \> \mwedge{} No-dup-deliver$_{\mbox{\small {E}}}$))) \end{program*}$
The following recursively defined relation on lists holds when the two lists agree on the order of the elements they have in common.
$\begin{program*} \> \\ \> agree\_on\_common(T;as;bs) ==\\ \> case as of \\ \>... ...) \mwedge{} agree\_on\_common(T;as';bs')) \\ \> esac \\ \> esac \end{program*}$
The total-order property is defined by
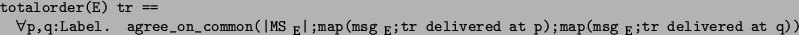
$\begin{program*} \> \\ \> totalorder(E) tr ==\\ \> \mforall{}p,q:Label. agree\... ...delivered at p);map(msg$_{\mbox{\small {E}}}$;tr delivered at q)) \end{program*}$
This says that the lists of messages delivered to any two locations agree on the order of messages that they have in common. This property is a ``local-deliver-property''. It only depends on some relation on the lists tr delivered at p.
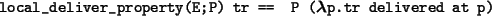
$\begin{program*} \> \\ \> local\_deliver\_property(E;P) tr == P (\mlambda{}p.tr delivered at p) \end{program*}$

We can show that any such property is switchable, provided the relation on the local delivery lists satisfies some closure conditions.
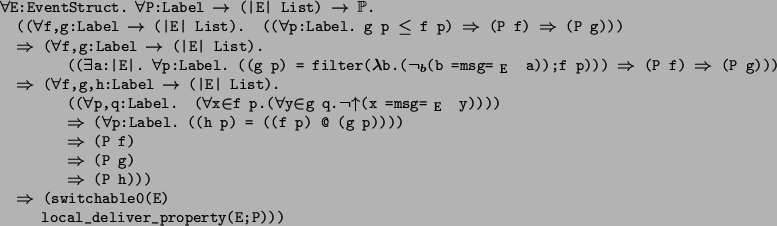
$\begin{program*} \> \\ \> \mforall{}E:EventStruct. \mforall{}P:Label {}\mrighta... ...ghtarrow{} (switchable0(E) \\ \> local\_deliver\_property(E;P))) \end{program*}$
Using this theorem, we check the closure conditions for the relation that defines total order, and all the conditions are met. So we have:
$\begin{program*} \> \\ \> \mforall{}E:EventStruct\\ \> (switchable$_{\mbox{\sm... ...all {E}}}$\\ \> \mwedge{} No-dup-deliver$_{\mbox{\small {E}}}$)) \end{program*}$

Next: About this document ... Up: Proof of the Switch Previous: Proof of the Switch

Richard Eaton 2002-02-20