Proof of the Switch Theorem

We said that theorem 5.7 is essentially our main result, but it is a theorem about trace properties over a tagged event structure, and the fusion condition that is its conclusion is a condition on a single tagged trace. Our real main result will be about properties over an event structure, and the hypotheses will relate two traces, the traces ``above'' and ``below'' our switching protocol layer. The upper trace tr$_{u}$ will be a trace over an event structure E, so it is a list of send and deliver events. The lower trace tr$_{l}$ will be a list of some actions of a type A. These actions represent the channels between the switch layer and the different protocols being switched. Each of these actions is essentially a pair of an event from |E| and a label. That is, from an action a A we can extract its event and a label identifying which protocol it is for. So we have functions evt A |E| and tg A Label. From these functions, we can form a tagged event structure over A as follows:

If tr$_{l}$ is a list of actions in A, then map(evt;tr$_{l}$) is a list of events in |E|, i.e a trace over E. Thus, if P is a trace property over E then we define

and P is a trace property over the induced tagged event structure <A,evt,tg>. Using these definitions and theorem 5.7 we get:

proof: This follows from theorem 5.7 and the definition of fusion, once we establish that (switchable $_{\mbox{\small {E}}}$ P) (switchable $_{\mbox{\small {<A,evt,tg>}}}$ P) and (No-dup-send $_{\mbox{\small {E}}}$ map(evt;tr$_{l}$)) (No-dup-send $_{\mbox{\small {<A,evt,tg>}}}$ tr$_{l}$). Both of these follow easily from the facts that the map operation commutes with every list operation used in the definitions of switchable $_{\mbox{\small {E}}}$ and No-dup-send $_{\mbox{\small {E}}}$, and that, by definition, evt, maps the event structure of A to E.

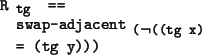
The switching protocol layer delays the delivery of messages from one sub-protocol until the messages from the previous sub-protocol have been delivered. It thus reorders the trace of tagged events (the actions A) in its lower trace tr$_{l}$ so that the reordered trace, which we call tr$_{m}$, for the middle trace, satisfies the switch_inv $_{\mbox{\small {<A,evt,tg>}}}$ property. In this reordering, the switch does not change the ordering of actions from the same protocol, it only changes the ordering of actions from different protocols. Thus, the lower and middle traces, tr$_{l}$ and tr$_{m}$, will be related by the following tag relation

With the tags removed, the reordered actions in tr$_{m}$ are the same as the events in the upper trace tr$_{u}$, except that further delays in the switch may change the order of these events, and the upper trace tr$_{u}$ may contain additional send events that have not yet been communicated through the switch to the lower (or middle) trace. Thus, map(evt;tr$_{m}$) is related to tr$_{u}$ by the layer relation:

Putting all of these things together, we have the following definition of the full invariant that the switch layer must guarantee.

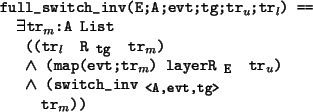
We can finally derive our main theorem.

proof: We use theorem 6.1 with tr$_{m}$ for tr. We must show

which follows from the assumption No-dup-send $_{\mbox{\small {E}}}$ tr$_{u}$ and the easy lemma that No-dup-send $_{\mbox{\small {E}}}$ is preserved by layerR $_{\mbox{\small {E}}}$. We must also show that

which follows from the assumption m:Label. (P map(evt;tr$_{l}$$\mid$)) and the easy lemma that

The conclusion of theorem 6.1 then gives us P map(evt;tr$_{m}$) and we must show P tr$_{u}$. But this follows from fact that P is preserved by the layer relation and map(evt;tr$_{m}$) layerR $_{\mbox{\small {E}}}$ tr$_{u}$, by the full_switch_inv assumption.