Removing the Normal Form Requirement

The conclusion of theorem 5.4 has the form ((I J) K) fuses P, where J is the normal form property AD-normal $_{\mbox{\small {E}}}$. We show that if P is asynchronous and delayable, then we can remove this requirement and prove (I K) fuses P. An asynchronous, delayable property P is preserved by the following relation

This relation is a symmetric relation and also has the property that we call tag-splitable. If two traces are related by adR $_{\mbox{\small {E}}}$, then so are their tagged subtraces for any given tag.





proof: The reason that adR $_{\mbox{\small {E}}}$ is tag-splitable is that it is the transitive closure of relations defined by swapping adjacent elements. If tr$_{1}$ is obtained from tr$_{2}$ by swapping adjacent elements, then tr$_{1}$$\mid$ will either be equal to tr$_{2}$$\mid$ (if the two elements swapped do not both have tag m) or else obtained by swapping adjacent elements of tr$_{2}$$\mid$.

The outline of the argument we use to remove the normal form requirement is contained in the following lemma.



proof: If tr has properties I and K, and if m:Label. (P tr$\mid$), then we must show P tr assuming the six hypotheses. Using the fifth hypothesis, we find tr', related to tr by R and satisfying I and J. Since R preserves K, trace tr' also satisfies K. Using the fusion hypothesis, we can conclude that P tr' if we can show m:Label. (P tr'$\mid$). This follows from the assumptions that R is tag-splitable and preserves P. Once we have P tr', we conclude P tr from the assumptions that R is a symmetric relation and preserves P.

The K we need in the previous argument is No-dup-send $_{\mbox{\small {E}}}$, and the R is adR $_{\mbox{\small {E}}}$. That R preserves K follows from the next two lemmas whose proofs are straightforward.







When we instantiate lemma 5.4.2 with K and R as above and with switch_inv $_{\mbox{\small {E}}}$ for I and AD-normal $_{\mbox{\small {E}}}$ for J, then the last hypothesis is theorem 5.4, and, as we have seen, the first four hypotheses are all satisfied. The fifth hypothesis becomes the following lemma, which we will prove.



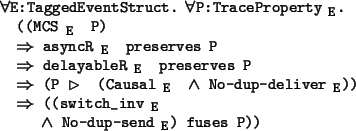
Once lemma 5.4.5 is proved, we see that we have the following theorem, which is essentially our main result.

Proof of lemma 5.4.5 : We use the following general theorem on the existence of partially sorted lists. It says that by swapping adjacent elements x,y of list L, for which (P x y), provided that each swap results in a pair that satisfies P, we may reach a sorted list L' in which all adjacent pairs satisfy P.




proof: The proof is by induction on the cardinality of the set of bad pairs- the pairs for which (P x y) and where x precedes y in L (but is not necessarily adjacent). If P is decidable, we can find an adjacent bad pair, if one exists, and show that swapping decreases the cardinality of the set of bad pairs.

We apply theorem 5.6 with P instantitated to

We must show that ad-normalR $_{\mbox{\small {tr}}}$ is decidable, which is easy, and that

This follows from the No-dup-send $_{\mbox{\small {E}}}$ property of tr, since if (a,b) is a pair of out of order deliveries then (b,a) will not be out of order since there are unique send events for them. The partial sort theorem then gives us a trace tr' reachable from trace tr by swapping adjacent pairs for which (ad-normalR $_{\mbox{\small {tr}}}$ a b), and for which all adjacent pair satisfy ad-normalR $_{\mbox{\small {tr}}}$. We must show that tr adR $_{\mbox{\small {E}}}$ tr', that switch_inv $_{\mbox{\small {E}}}$ tr', and that AD-normal $_{\mbox{\small {E}}}$ tr'. The first of these follows from the observation that swapping adjacent pairs for which (ad-normalR $_{\mbox{\small {tr}}}$ a b) always swaps pairs allowed by either the relation asyncR $_{\mbox{\small {E}}}$ or the relation delayableR $_{\mbox{\small {E}}}$. The second requirement follows from the assumption that switch_inv $_{\mbox{\small {E}}}$ tr, and the following lemma, whose proof is straightforward, which shows that swapping pairs for which (ad-normalR $_{\mbox{\small {tr}}}$ a b) preserves the property switch_inv $_{\mbox{\small {E}}}$.



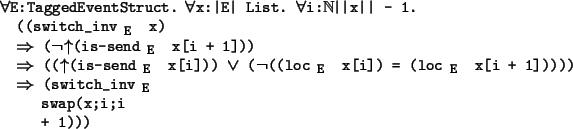
To finish the proof of lemma 5.4.5 it remains to show that if all adjacent element of tr' satisfy ad-normalR $_{\mbox{\small {tr}}}$ then tr' satisfies AD-normal $_{\mbox{\small {E}}}$ . It can easily be seen that if all adjacent pairs satisfy ad-normalR $_{\mbox{\small {tr'}}}$ then tr' is in normal form. But the dependence of ad-normalR $_{\mbox{\small {tr}}}$ on parameter tr is only on the order of send events in tr, and this order is preserved by the swaps that lead from tr to tr'.

We restate theorem 5.5 by combining its hypotheses into the definition of a switchable property.