


Next: Memoryless-Composable Induction
Up: hybrid_protocol_paper_obj
Previous: Tagged Events
Fusion of Trace Properties
If the protocol associated with each label is guaranteeing some trace property
P, and tr is a trace, then we will have m:Label. (P tr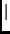 ).
A switch protocol must guarantee some additional property I that is
strong enough to guarantee that property P holds of the whole trace tr.
If this is the case for I and P then we say that I is a
fusion condition for P, and we define
).
A switch protocol must guarantee some additional property I that is
strong enough to guarantee that property P holds of the whole trace tr.
If this is the case for I and P then we say that I is a
fusion condition for P, and we define

We will be looking for properties I that are fusion conditions for
whole classes of trace properties P. We will show that certain properties
are fusion conditions for all properties P that satisfy certain
meta-properties.
We start this investigation with some simple lemmas about fusion.
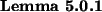

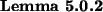

![\begin{lemma}[fusion simplification]
\ignorelabel{O16396cf442326fbe0d7d5f188489}
\end{lemma}](img49.png)

The proofs of these lemmas are straightforward.
We will also need a few lemmas about fusion conditions for the properties
Causal
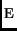 and No-dup-deliver
and No-dup-deliver
 .
.
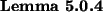
proof: This lemma says that if m:Label. (Causal
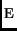 tr
tr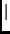 ) then
Causal
) then
Causal
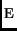 tr. To show this, let tr[j] be a member of tr. We must
show that there is an i j such that tr[i] is
the send event for tr[j]. Event tr[j] has some tag m and using the
causal property on tr
tr. To show this, let tr[j] be a member of tr. We must
show that there is an i j such that tr[i] is
the send event for tr[j]. Event tr[j] has some tag m and using the
causal property on tr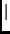 , we find a send event x for tr[j] in tr
, we find a send event x for tr[j] in tr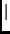 .
Since tr
.
Since tr is a sublist of tr, event x also precedes
j in the trace tr.
is a sublist of tr, event x also precedes
j in the trace tr.
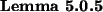
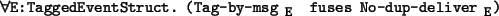
proof: If trace tr has a duplicate delivery of the message in event x,
then trace tr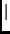 , where m = (tag
, where m = (tag
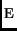 x), also has a duplicate delivery
because, if tr has the Tag-by-msg
x), also has a duplicate delivery
because, if tr has the Tag-by-msg
 property,
all the relevant events have the same tag, m.
property,
all the relevant events have the same tag, m.
proof: If x is an event in tr, it has tag m = (tag
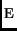 x) and since
tr
x) and since
tr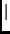 is causal, there is a send event for x with tag m. So any
event x has a send event with the same tag. If tr has the
No-dup-send
is causal, there is a send event for x with tag m. So any
event x has a send event with the same tag. If tr has the
No-dup-send
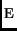 property, then any two events with the same message must
have the same send event and therefore the same tag.
property, then any two events with the same message must
have the same send event and therefore the same tag.
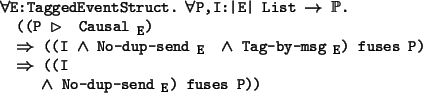
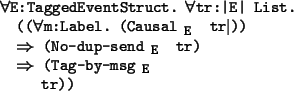
proof: This follows easily from lemma 5.0.6.

proof: By lemma 5.0.7, it is enough to show that
(I No-dup-send
 Tag-by-msg
Tag-by-msg
 ) fuses P. Then using the fusion
simplification
lemma 5.0.3 with J = (Causal
) fuses P. Then using the fusion
simplification
lemma 5.0.3 with J = (Causal
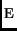 No-dup-deliver
No-dup-deliver
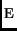 ),
it is enough to show that
),
it is enough to show that
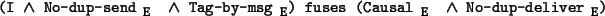
This follows from
lemma 5.0.1, lemma 5.0.2,
lemma 5.0.4, and lemma 5.0.5.
Subsections



Next: Memoryless-Composable Induction
Up: hybrid_protocol_paper_obj
Previous: Tagged Events
Richard Eaton
2002-02-20







![]()