The Switch Invariant

The switch guarantees that if two messages are sent using different protocols, then before the second message is delivered at any location, the first message must already have been delivered at that location. Thus, the switch guarantees the following invariant.

We will show that certain strengthening of this invariant refines the switch-decomposablity property. This will be the crucial step in the proof of the main theorem. To accomplish this step, we first reformulate the switch invariant in a form that is more convienient for the argument. We now define a key relation switchR $_{\mbox{\small {tr}}}$. It relates two times i and j if the events at those times were send events and their messages were delivered out of order at some location. Note that switchR $_{\mbox{\small {tr}}}$ is a symmetric relation on the times ||tr||.

The switch invariant says that events whose times are related by switchR $_{\mbox{\small {tr}}}$ must have the same tag. So, using simple logic, we can prove

We want to show that a strengthening of switch_inv $_{\mbox{\small {E}}}$ refines switch-decomposable $_{\mbox{\small {E}}}$ . For a non null trace tr satisfying switch_inv $_{\mbox{\small {E}}}$ tr we must find the criterion Q on the times ||tr|| that satisfies the five properties in the definition of switch-decomposability. If tr also satisfies Causal $_{\mbox{\small {E}}}$ tr then it must contain a send event and hence there must be a time ls which is the time of the last send event in tr. We will define Q to hold on all times related to ls by switchR $_{\mbox{\small {tr}}}$.

It is fairly easy to show that Q has the first four of the five required properties. First, Q is decidable because switchR $_{\mbox{\small {tr}}}$ is decidable and the transitive closure of a decidable relation over a finite domain is also decidable. Second, Q is non empty beacause Q ls holds. The third requirement follows from the the fact that ls is the time of a send event and the following lemma, which is proved by induction on the transitive closure from the fact that switchR $_{\mbox{\small {tr}}}$ relates only times of send events.

Similarly, the fourth requirement, that the events of times satisfying Q all have the same tag, is a consequence of the following lemma, proved by induction from lemma 5.3.1.

It remains only to establish the fifth property of Q, namely,

To prove this property of Q we will need a stronger invariant than the property switch_inv $_{\mbox{\small {E}}}$ Causal $_{\mbox{\small {E}}}$ used so far. Without strengthening the invariant we can prove a weaker version of the requirement. We can prove

This establishes the requirement for the case when the event at time j is a send event, and we need this lemma to prove the full requirement. For this lemma, the only assumption we need is that ls is the time of the last send event.



proof: We assume that ls is the time of the last send, that i j, that (is-send $_{\mbox{\small {E}}}$ tr[j]), and that i (switchR $_{\mbox{\small {tr}}}$) ls. So, for some n, i switchR $_{\mbox{\small {tr}}}$ $^{\mbox{\small {n}}}$ ls, and we prove by induction on n that j (switchR $_{\mbox{\small {tr}}}$) ls. When n = 0, then i = ls, so ls j. Since ls is the last send, we have j = ls and hence, j (switchR $_{\mbox{\small {tr}}}$) ls. Now 0 < n, and i switchR $_{\mbox{\small {tr}}}$ $^{\mbox{\small {n}}}$ ls, so by definition, there is a time z such that
i switchR $_{\mbox{\small {tr}}}$ z and z switchR $_{\mbox{\small {tr}}}$ $^{\mbox{\small {n - 1}}}$ ls. If z j, then by induction, j (switchR $_{\mbox{\small {tr}}}$) ls. So, we may assume j < z. Also, if j = i, then we have j (switchR $_{\mbox{\small {tr}}}$) ls, by hypothesis. So, we may assume i < j. So we also have i < z, and since i switchR $_{\mbox{\small {tr}}}$ z, we must have tr[z] somewhere delivered before tr[i]. Then by lemma 4.3.1, we have tr[z] somewhere delivered before tr[j] tr[j] somewhere delivered before tr[i]. In the first case, because j < z we have j switchR $_{\mbox{\small {tr}}}$ z and hence j switchR $_{\mbox{\small {x}}}$ $^{\mbox{\small {n}}}$ ls. In the second case, because i < j we have j switchR $_{\mbox{\small {tr}}}$ i and hence j switchR $_{\mbox{\small {tr}}}$ $^{\mbox{\small {n + 1}}}$ ls. So, in either case, j (switchR $_{\mbox{\small {tr}}}$) ls and we are done.

To prove the complete closure requirement, i,j:||tr||. ((Q i) (i j) (C(Q) j)), we will have to assume that the trace tr has a certain normal form. We will be able to put a trace into normal form using only operations that preserve the relation asyncR $_{\mbox{\small {E}}}$ delayableR $_{\mbox{\small {E}}}$. So, for asynchronous, delayable properties, P, if P holds of the normal form of trace tr, then it also holds of tr.

We put a trace into normal form by moving send events as late as possible and by reordering asynchronous deliver events to match the order of their send events. More constructively, we apply the following normalization algorithm. If we find an adjacent pair of events (a,b) in the trace where a is a send event and b is a deliver event, then, unless they contain the same message, we swap the two events so that the send event a occurs later than the deliver event b. If we find an adjacent pair of deliver events (a,b) for which there are corresponding send events that occur in the opposite order, then if events a and b are at different locations, we swap them so that their order is the same as their corresponding send events. Under some additional assumptions, we will prove that this algorithm terminates and results in a trace that satisfies the following normal form property, that we call asynchronous-delayable normal form or AD-normal.

Assuming that trace tr satisfies AD-normal $_{\mbox{\small {E}}}$ and two additional properties, No-dup-deliver $_{\mbox{\small {E}}}$ and Causal $_{\mbox{\small {E}}}$, and the assumptions needed for lemma 5.3.4, we can now prove

proof: We proceed by induction on j - i. If (j - i) = 0, then j = i, so Q j, and hence C(Q) j. If (j - i) > 0, then i (j - 1). We assume Q i, and this implies that tr[i] is a send event. We must show C(Q) j. If the event at time j is a send event, then lemma 5.3.4 implies that Q j. So we may assume that tr[j] is a deliver event. case 1 tr[j - 1] is a send event. Lemma 5.3.4 implies that Q (j - 1) and the normal form implies that (tr[j - 1] =msg= $_{\mbox{\small {E}}}$ tr[j]). Hence C(Q) j. case 2 tr[j - 1] is a deliver event. By induction, we have C(Q) (j - 1), so there is a time k such that Q k and the events at times k and j - 1 have the same message. So the event at time k is the send event for the deliver event at time j - 1. By the Causal $_{\mbox{\small {E}}}$ property, there is also a time j' when the send event for the delivery at time j occured. We claim that Q j' holds, and hence C(Q) j. case 2.1 j' < k. In this case, the deliveries at times j - 1 and j are out of order, so by the normal form property, they must have the same location, call it p. Since we have the No-dup-deliver $_{\mbox{\small {E}}}$ property, there cannot be any delivery of the message sent at time j' to location p other than the one at time j. Therefore we have tr[k] somewhere delivered before tr[j'], and this implies that j' switchR $_{\mbox{\small {tr}}}$ k. Since Q k, and since Q is closed under switchR $_{\mbox{\small {tr}}}$, we get Q j'. case 2.2 k j'. In this case, since the event at time j' is a send and since Q k, lemma 5.3.4 implies that Q j'.

Putting together everything we have proved in this section, we see that we have proved the following

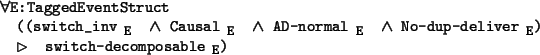
The next theorem combines all the previous lemmas.

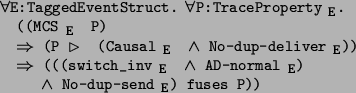
proof: Using lemma 5.0.8, it is enough to show that I fuses P where

We prove this using MCS-induction. The hypotheses of the MCS-induction require us to show that I is a safety property and that I is single-tag-decomposable. It is straightforward to show that each of the six conjoined properties in I is a safety property, and therefore I is a safety property. By theorem 5.2, to show that I is single-tag decomposable, it is enough to show that I is switch-decomposable, since I refines Tag-by-msg $_{\mbox{\small {E}}}$, Causal $_{\mbox{\small {E}}}$, and No-dup-send $_{\mbox{\small {E}}}$. But I refines

and, by theorem 5.3 , that property refines the switch-decomposabilty property.