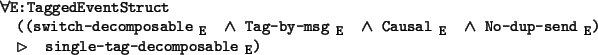Next: The Switch Invariant
Up: Fusion of Trace Properties
Previous: Memoryless-Composable Induction
Single-tag decomposabilty says that for a non null list of tagged events
there must exist a decomposition into two suitable lists.
We refine this property with a somewhat more constructive condition
that we call switch decomposability.
It says that for a non null list L of tagged events there must exist
a decidable criterion Q on the times (the list indices) that satisfies
a number of closure conditions.
We will use the criterion Q to partition the list into two parts by defining
the message closure of Q
![\begin{program*}
\> \\
\> C(Q) i ==\\
\> \mexists{}k:\mBbbN{}\vert\vert L\vert...
...e{} (\muparrow{}(L[k] \\
\> =msg=$_{\mbox{\small {E}}}$\ L[i])))
\end{program*}](img65.png)
and then partitioniong L into L-CQ, containing those L[i] for which C(Q) i,
and L-notCQ, the rest.

We show that this property is a refinement of the single-tag decomposability
in the following
proof:
We have a switch-decomposable list L that also satisfies the other three
properties and, if L is non null we must produce a single-tag decomposition.
In this case there is a Q with the properties given in the definition of switch-decomposable.
The first of these properties says that Q i is decidable. From this, we can
show that
C(Q) i is also decidable, and therefore we can filter L on C(Q) and C(Q) to
get L = L-notCQ and L
= L-notCQ and L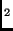 = L-CQ. We claim that this is a single-tag
decomposition of L. We have to show that
L
= L-CQ. We claim that this is a single-tag
decomposition of L. We have to show that
L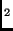 is non null, that L
is non null, that L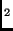 is a final segment of L,
that L
is a final segment of L,
that L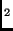 has only one tag, and that L
has only one tag, and that L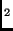 and L
and L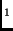 have no messages in common.
From the second property of Q we see that L
have no messages in common.
From the second property of Q we see that L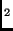 is non null.
By definition of the message closure, C(Q), every event in L that has the
same message as an event in L
is non null.
By definition of the message closure, C(Q), every event in L that has the
same message as an event in L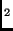 must also be in L
must also be in L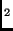 . Therefore L
. Therefore L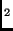 and
L
and
L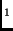 can have no messages in common.
The fourth property of Q says that all events L[i] for which Q i holds,
have the same tag. Everything in L
can have no messages in common.
The fourth property of Q says that all events L[i] for which Q i holds,
have the same tag. Everything in L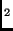 has the same message as one of these,
so from the Tag-by-msg
has the same message as one of these,
so from the Tag-by-msg
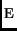 property of L, we deduce that everything in
L
property of L, we deduce that everything in
L has the same tag.
To see that L
has the same tag.
To see that L is a final segment of L, suppose that C(Q) i and i j.
We must show that C(Q) j. Using the fifth property of Q,
it's enough to find an i' with (i' i) (Q i').
But, by definition, (C(Q) i) (k:||L||. ((Q k) ((L[k] =msg=
is a final segment of L, suppose that C(Q) i and i j.
We must show that C(Q) j. Using the fifth property of Q,
it's enough to find an i' with (i' i) (Q i').
But, by definition, (C(Q) i) (k:||L||. ((Q k) ((L[k] =msg=
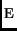 L[i])))).
We are done if we show that any such k satisfies k i. This follows from
the third property of Q, which implies that L[k] is a send event, and
the two properties, No-dup-send
L[i])))).
We are done if we show that any such k satisfies k i. This follows from
the third property of Q, which implies that L[k] is a send event, and
the two properties, No-dup-send
 and Causal
and Causal
 ,
which imply that for every event L[i] there is a unique send event with the same
message, and that that send event must occur before i.
,
which imply that for every event L[i] there is a unique send event with the same
message, and that that send event must occur before i.



Next: The Switch Invariant
Up: Fusion of Trace Properties
Previous: Memoryless-Composable Induction
Richard Eaton
2002-02-20
![\begin{program*}
\> \\
\> C(Q) i ==\\
\> \mexists{}k:\mBbbN{}\vert\vert L\vert...
...e{} (\muparrow{}(L[k] \\
\> =msg=$_{\mbox{\small {E}}}$\ L[i])))
\end{program*}](img65.png)