We are looking for a metaproperty switchable
![]() and a property switch_inv
and a property switch_inv
![]() such that switch_inv
such that switch_inv
![]() is a fusion condition for any
property P that satisfies switchable
is a fusion condition for any
property P that satisfies switchable
![]() P. We find this pair by a sequence of
refinements.
P. We find this pair by a sequence of
refinements.
We begin by assuming that P will be a memoryless, composable, safety property.
So it satisfies the metaproperty
![]()
We can now define a basic condition, single-tag decomposable,
that fuses any MCS property.

It says that any non null trace L can be decomposed as the append of two lists,
L![]() and L
and L![]() , such that the two lists have no messages in common and the
second list L
, such that the two lists have no messages in common and the
second list L![]() is non null and all events in it have the same tag.
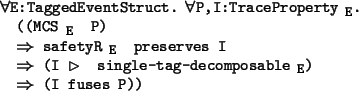
The MCS induction theorem states that a single-tag decomposable, safety property
is a fusion condition for any MCS property.
is non null and all events in it have the same tag.
The MCS induction theorem states that a single-tag decomposable, safety property
is a fusion condition for any MCS property.
![]()
proof:
We have to prove that (I tr) (P tr) under the assumptions that
m:Label. (P tr![]() ) and the other hypotheses in the theorem.
We proceed by induction on the length of tr.
If tr has length 0, then it is the null list. Then,
for any label m, tr
) and the other hypotheses in the theorem.
We proceed by induction on the length of tr.
If tr has length 0, then it is the null list. Then,
for any label m, tr![]() = tr, so P tr by hypothesis.
Now tr is non null. Since I tr, and since I refines
single tag decomposability, we can find message-disjoint tr
= tr, so P tr by hypothesis.
Now tr is non null. Since I tr, and since I refines
single tag decomposability, we can find message-disjoint tr![]() and tr
and tr![]() such that tr = (tr
such that tr = (tr![]() @ tr
@ tr![]() ) and tr
) and tr![]() is non null and has only one tag.
Since the length of tr
is non null and has only one tag.
Since the length of tr![]() is less than the length of tr, we can apply
the induction hypothesis to conclude that P tr
is less than the length of tr, we can apply
the induction hypothesis to conclude that P tr![]() provided that we can show
that I tr
provided that we can show
that I tr![]() and m:Label. (P tr
and m:Label. (P tr![]()
![]() ). The first of these follows from the
assumption that I is a safety property, and the second follows from the
assumption that P is a safety property and from the fact that
m:Label. (tr
). The first of these follows from the
assumption that I is a safety property, and the second follows from the
assumption that P is a safety property and from the fact that
m:Label. (tr![]() tr tr
tr tr![]()
![]() tr
tr![]()
![]() ).
Since P is a composable property, we can conclude P tr if we can show
P tr
).
Since P is a composable property, we can conclude P tr if we can show
P tr![]() . By assumption, there is a tag m such that tr
. By assumption, there is a tag m such that tr![]() = tr
= tr![]()
![]() ,
so it's enough to show P tr
,
so it's enough to show P tr![]()
![]() . But tr
. But tr![]() = (tr
= (tr![]()
![]() @ tr
@ tr![]()
![]() ) and
tr
) and
tr![]() and tr
and tr![]() have no messages in common, and therefore tr
have no messages in common, and therefore tr![]()
![]() can
be obtained by removing all messages in tr
can
be obtained by removing all messages in tr![]() from tr
from tr![]() . Since P tr
. Since P tr![]() is
true by assumption and since P is memoryless, we can conclude that P tr
is
true by assumption and since P is memoryless, we can conclude that P tr![]()
![]() and we are done.
and we are done.