Thm*  l:T List, x,y,z:T. l:T List, x,y,z:T.
Thm* no_repeats(T;l)   x before y x before y  l l   y before z y before z  l l   x before z x before z  l l | [l_before_transitivity] |
Thm*  L1,L2,L:T List, x:T. L1,L2,L:T List, x:T.
Thm* no_repeats(T;L)   L1 @ [x] L1 @ [x] 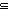 L L   [x / L2] [x / L2] 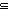 L L   L1 @ [x / L2] L1 @ [x / L2] 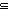 L L | [append_overlapping_sublists] |
Thm*  l:T List. no_repeats(T;l) l:T List. no_repeats(T;l) 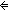  ( ( x,y:T. x before y x,y:T. x before y  l l   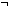 x = y) x = y) | [no_repeats_iff] |
Thm*  as:T1 List, bs:T2 List. ||as|| = ||bs|| as:T1 List, bs:T2 List. ||as|| = ||bs||  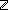   unzip(zip(as;bs)) = <as,bs> unzip(zip(as;bs)) = <as,bs> | [unzip_zip] |
Thm*  as:T1 List, bs:T2 List. ||as|| = ||bs|| as:T1 List, bs:T2 List. ||as|| = ||bs||  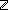   ||zip(as;bs)|| = ||as|| ||zip(as;bs)|| = ||as||  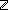 | [length_zip] |
Thm*  as:T1 List, bs:T2 List, i: as:T1 List, bs:T2 List, i: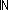 . .
Thm* i<||zip(as;bs)||   zip(as;bs)[i] = <as[i],bs[i]> zip(as;bs)[i] = <as[i],bs[i]> | [select_zip] |
Thm*  L_1,L_2:T List. L_1 L_1,L_2:T List. L_1  L_2 L_2   L_1 L_1 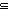 L_2 L_2 | [iseg_is_sublist] |
Thm*  l1,l2:T List. l1 l1,l2:T List. l1  l2 l2   ||l1|| ||l1|| ||l2|| ||l2|| | [iseg_length] |
Thm*  P:(T P:(T 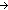 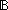 ), L2,L1:T List. L1 ), L2,L1:T List. L1  L2 L2   filter(P;L1) filter(P;L1)  filter(P;L2) filter(P;L2) | [filter_iseg] |
Thm*  l1,l2:T List, x:T. l1 l1,l2:T List, x:T. l1  l2 l2   (x (x  l1) l1)   (x (x  l2) l2) | [iseg_member] |
Thm*  l1,l2:T List. l1 l1,l2:T List. l1  l2 l2 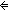  ||l1|| ||l1|| ||l2|| & ( ||l2|| & ( i: i: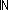 . i<||l1|| . i<||l1||   l1[i] = l2[i]) l1[i] = l2[i]) | [iseg_select] |
Thm*  l1,l2,l3:T List. l2 l1,l2,l3:T List. l2  l3 l3   l1 l1  l2 l2   l1 l1  l3 l3 | [iseg_transitivity2] |
Thm*  l1,l2,l3:T List. l1 l1,l2,l3:T List. l1  l2 l2   l1 l1  l2 @ l3 l2 @ l3 | [iseg_append] |
Thm*  l1,l2,l3:T List. l1 l1,l2,l3:T List. l1  l2 l2   l2 l2  l3 l3   l1 l1  l3 l3 | [iseg_transitivity] |
Thm*  L:A List, f1,f2:(A L:A List, f1,f2:(A 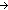 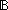 ). f1 = f2 ). f1 = f2   (filter(f1;L) ~ filter(f2;L)) (filter(f1;L) ~ filter(f2;L)) | [filter_functionality] |
Thm*  L:T List, a,b:T. a before b L:T List, a,b:T. a before b  L L   (a (a  L) L) | [l_before_member2] |
Thm*  L:T List, a,b:T. a before b L:T List, a,b:T. a before b  L L   (b (b  L) L) | [l_before_member] |
Thm*  x,y:T, L:T List. x,y:T, L:T List.
Thm* (x  L) L)   (y (y  L) L)   x = y x = y 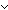 x before y x before y  L L 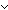 y before x y before x  L L | [l_tricotomy] |
Thm*  L:T List, i,j: L:T List, i,j: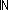 ||L||. i<j ||L||. i<j   [L[i]; L[j]] [L[i]; L[j]] 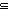 L L | [sublist_pair] |
Thm*  L1,L2:T List. L1,L2:T List. 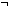 null(L2) null(L2)   L1 L1 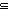 tl(L2) tl(L2)   L1 L1 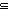 L2 L2 | [sublist_tl] |
Thm*  L1,L2:T List. L1 = L2 L1,L2:T List. L1 = L2   L1 L1 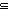 L2 L2 | [sublist_weakening] |
Thm*  L1,L2:T List. L1 L1,L2:T List. L1 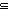 L2 L2   L2 L2 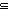 L1 L1   L1 = L2 L1 = L2 | [sublist_antisymmetry] |
Thm*  L1,L2:T List. L1 L1,L2:T List. L1 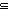 L2 L2   ||L1|| = ||L2|| ||L1|| = ||L2||  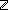   L1 = L2 L1 = L2 | [proper_sublist_length] |
Thm*  L1,L2:T List. L1 L1,L2:T List. L1 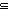 L2 L2   ||L1|| ||L1|| ||L2|| ||L2|| | [length_sublist] |
Thm*  L1,L2,L3:T List. L1 L1,L2,L3:T List. L1 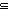 L2 L2   L2 L2 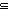 L3 L3   L1 L1 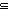 L3 L3 | [sublist_transitivity] |
Thm*  L:T List, x:T. L:T List, x:T. 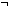 null(L) null(L)   last([x / L]) = last(L) last([x / L]) = last(L) | [last_cons] |
Thm*  T:Type, L:T List. T:Type, L:T List. 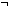 null(L) null(L)   last(L) last(L)  T T | [last_wf] |
Thm*  x:T, l:T List. ( x:T, l:T List. ( y:T. Dec(x = y)) y:T. Dec(x = y))   Dec((x Dec((x  l)) l)) | [l_member_decidable] |
Thm*  L:T List, x:T. (x L:T List, x:T. (x  L) L)   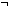 null(L) null(L) | [member_null] |
Thm*  L:T List, x:T. null(L) L:T List, x:T. null(L)   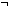 (x (x  L) L) | [null_member] |
Thm*  as:T List, x:T. 0<||as|| as:T List, x:T. 0<||as||   (x (x  tl(as)) tl(as))   (x (x  as) as) | [member_tl] |
Thm*  a:T List, f:(T a:T List, f:(T 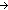 T). ( T). ( x:T. (x x:T. (x  a) a)   f(x) = x) f(x) = x)   map(f;a) = a map(f;a) = a | [trivial_map] |
Thm*  a:T List, f,g:(T a:T List, f,g:(T 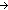 T'). T').
Thm* ( x:T. (x x:T. (x  a) a)   f(x) = g(x)) f(x) = g(x))   map(f;a) = map(g;a) map(f;a) = map(g;a) | [map_equal2] |
Thm*  L:T List. L:T List. 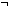 L = nil L = nil   ( (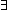 x:T. (x x:T. (x  L)) L)) | [member_exists] |
Thm*  z:T List. ||z|| = 2 z:T List. ||z|| = 2  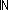   z = [z[0]; z[1]] z = [z[0]; z[1]] | [list_2_decomp] |
Thm*  Q:((T List) Q:((T List) 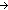 Prop). Prop).
Thm* Q(nil)   ( ( ys:T List, x:T. Q(ys) ys:T List, x:T. Q(ys)   Q(ys @ [x])) Q(ys @ [x]))   ( ( zs:T List. Q(zs)) zs:T List. Q(zs)) | [list_append_singleton_ind] |
Thm*  L:T List. 0<||L|| L:T List. 0<||L||   ( (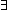 x:T, L':T List. L = (L' @ [x])) x:T, L':T List. L = (L' @ [x])) | [list_decomp_reverse] |
Thm*  a:T List, f,g:(T a:T List, f,g:(T 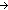 T'). T').
Thm* ( i: i: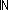 . i<||a|| . i<||a||   f(a[i]) = g(a[i])) f(a[i]) = g(a[i]))   map(f;a) = map(g;a) map(f;a) = map(g;a) | [map_equal] |
Thm*  a,b:T List. ||a|| = ||b|| a,b:T List. ||a|| = ||b||  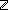   ( ( i: i: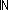 . i<||a|| . i<||a||   a[i] = b[i]) a[i] = b[i])   a = b a = b | [list_extensionality] |
Thm*  m: m: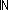 , L:T List. m<||L|| , L:T List. m<||L||   (nth_tl(m;L) ~ [L[m] / nth_tl(1+m;L)]) (nth_tl(m;L) ~ [L[m] / nth_tl(1+m;L)]) | [nth_tl_decomp] |
Thm*  L:T List. 0<||L|| L:T List. 0<||L||   (L ~ [hd(L) / tl(L)]) (L ~ [hd(L) / tl(L)]) | [list_decomp] |
Thm*  L:T List. L:T List. 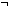 L = nil L = nil   0<||L|| 0<||L|| | [non_nil_length] |
Thm*  L:T List, P:( L:T List, P:(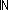 ||L|| ||L|| 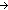 Prop). Prop).
Thm* ( x: x: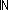 ||L||. Dec(P(x))) ||L||. Dec(P(x)))
Thm*  
Thm* ( i,j: i,j: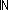 ||L||. P(i) ||L||. P(i)   i<j i<j   P(j)) P(j))
Thm*  
Thm* (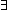 L_1,L_2:T List. L = (L_1 @ L_2) & ( L_1,L_2:T List. L = (L_1 @ L_2) & ( i: i: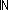 ||L||. P(i) ||L||. P(i) 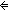  ||L_1|| ||L_1|| i)) i)) | [append_split2] |
Def no_repeats(T;l) ==  i,j: i,j: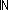 . i<||l|| . i<||l||   j<||l|| j<||l||   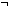 i = j i = j   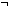 l[i] = l[j] l[i] = l[j]  T T | [no_repeats] |