Thm*  L:T List, P:(T L:T List, P:(T  T T  Prop). Prop).
Thm* ( x,y:T. Dec(P(x,y))) x,y:T. Dec(P(x,y)))
Thm*  
Thm* ( x,y:T. x,y:T.  P(x,y) P(x,y)   P(y,x)) P(y,x))
Thm*  
Thm* ( L':T List. L':T List.
Thm* ((L (swap adjacent[ P(x,y)]^*) L') & ( P(x,y)]^*) L') & ( i: i: (||L'||-1). P(L'[i],L'[(i+1)]))) (||L'||-1). P(L'[i],L'[(i+1)]))) | [partial_sort] |
Thm*  L:T List, P:(T L:T List, P:(T  T T  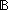 ). ).
Thm* ( x,y:T. P(x,y) x,y:T. P(x,y)    P(y,x)) P(y,x))
Thm*  
Thm* ( L':T List. L':T List.
Thm* ((L guarded_permutation(T;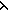 L,i. P(L[i],L[(i+1)])) L') L,i. P(L[i],L[(i+1)])) L')
Thm* (& ( i: i: (||L'||-1). (||L'||-1).  P(L'[i],L'[(i+1)]))) P(L'[i],L'[(i+1)]))) | [partial_sort_exists_2] |
Thm*  k: k: , x,y,z: , x,y,z: k. k.
Thm*  y = z y = z    x = y x = y   (x, y) = compose_list([(x, z); (y, z); (x, z)]) (x, y) = compose_list([(x, z); (y, z); (x, z)]) | [flip_lemma] |
Thm*  P:(L:(T List) P:(L:(T List)   (||L||-1) (||L||-1)  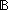 ), m:((T List) ), m:((T List)   ). ).
Thm* ( L:T List, i: L:T List, i: (||L||-1). (||L||-1).
Thm* (P(L,i)    P(swap(L;i;i+1),i) & m(swap(L;i;i+1))<m(L)) P(swap(L;i;i+1),i) & m(swap(L;i;i+1))<m(L))
Thm*  
Thm* ( L:T List. L:T List.
Thm* ( L':T List. L':T List.
Thm* ((L guarded_permutation(T;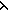 L,i. P(L,i)) L') & ( L,i. P(L,i)) L') & ( i: i: (||L'||-1). (||L'||-1).  P(L',i))) P(L',i))) | [partial_sort_exists] |
Thm*  L1,L2:T List, i,j: L1,L2:T List, i,j: ||L1||. ||L1||.
Thm* L2 = swap(L1;i;j)
Thm*  
Thm* L2[i] = L1[j] & L2[j] = L1[i] & ||L2|| = ||L1||   & L1 = swap(L2;i;j) & L1 = swap(L2;i;j)
Thm* & ( x: x: ||L2||. ||L2||.  x = i x = i    x = j x = j   L2[x] = L1[x]) L2[x] = L1[x]) | [swapped_select] |
Thm*  L:T List, P:( L:T List, P:( ||L|| ||L||  Prop). Prop).
Thm* ( x: x: ||L||. Dec(P(x))) ||L||. Dec(P(x)))
Thm*  
Thm* ( i: i: ||L||. P(i)) ||L||. P(i))   ( ( i: i: ||L||. P(i) & ( ||L||. P(i) & ( j: j: ||L||. i<j ||L||. i<j    P(j))) P(j))) | [last_with_property] |
Thm*  L:T List, P:( L:T List, P:( ||L|| ||L||  Prop). Prop).
Thm* ( x: x: ||L||. Dec(P(x))) ||L||. Dec(P(x)))
Thm*  
Thm* ( L1,L2:T List, f1:( L1,L2:T List, f1:( ||L1|| ||L1||   ||L||), f2:( ||L||), f2:( ||L2|| ||L2||   ||L||). ||L||).
Thm* (interleaving_occurence(T;L1;L2;L;f1;f2)
Thm* (& ( i: i: ||L1||. P(f1(i))) & ( ||L1||. P(f1(i))) & ( i: i: ||L2||. ||L2||.  P(f2(i))) P(f2(i)))
Thm* (& ( i: i: ||L||. ||L||.
Thm* (& ((P(i)   ( ( j: j: ||L1||. f1(j) = i)) ||L1||. f1(j) = i))
Thm* (& (& ( P(i) P(i)   ( ( j: j: ||L2||. f2(j) = i)))) ||L2||. f2(j) = i)))) | [interleaving_split] |
Thm*  P:(T P:(T  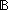 ), L:T List. ( ), L:T List. ( x x L. L. P(x)) P(x))   (filter(P;L) ~ nil) (filter(P;L) ~ nil) | [filter_is_nil] |
Def interleaving_occurence(T;L1;L2;L;f1;f2)
Def == ||L|| = ||L1||+||L2||  
Def == & increasing(f1;||L1||) & ( j: j: ||L1||. L1[j] = L[(f1(j))] ||L1||. L1[j] = L[(f1(j))]  T) T)
Def == & increasing(f2;||L2||) & ( j: j: ||L2||. L2[j] = L[(f2(j))] ||L2||. L2[j] = L[(f2(j))]  T) T)
Def == & ( j1: j1: ||L1||, j2: ||L1||, j2: ||L2||. ||L2||.  f1(j1) = f2(j2) f1(j1) = f2(j2)   ) ) | [interleaving_occurence] |
Def disjoint_sublists(T;L1;L2;L)
Def ==  f1:( f1:( ||L1|| ||L1||   ||L||), f2:( ||L||), f2:( ||L2|| ||L2||   ||L||). ||L||).
Def == increasing(f1;||L1||) & ( j: j: ||L1||. L1[j] = L[(f1(j))] ||L1||. L1[j] = L[(f1(j))]  T) T)
Def == & increasing(f2;||L2||) & ( j: j: ||L2||. L2[j] = L[(f2(j))] ||L2||. L2[j] = L[(f2(j))]  T) T)
Def == & ( j1: j1: ||L1||, j2: ||L1||, j2: ||L2||. ||L2||.  f1(j1) = f2(j2)) f1(j1) = f2(j2)) | [disjoint_sublists] |
Def l_disjoint(T;l1;l2) ==  x:T. x:T.  ((x ((x  l1) & (x l1) & (x  l2)) l2)) | [l_disjoint] |