| Rank | Theorem | Name |
| 6 | Thm*  L:T List, P:(T L:T List, P:(T  T T  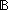 ), n: ), n: (||L||-1). (||L||-1).
Thm* count(x < y in swap(L;n;n+1) | P(x,y))
Thm* =
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)])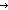 -1 else 0 fi+if P(L[(n+1)] -1 else 0 fi+if P(L[(n+1)]
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+if P,L[n]) -1 else 0 fi+if P,L[n])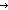
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+if 1 -1 else 0 fi+if 1
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+else 0 fi -1 else 0 fi+else 0 fi | [count_pairs_swap] |
| cites the following: |
| 3 | Thm*  L:T List, i,j: L:T List, i,j: ||L||. ||swap(L;i;j)|| = ||L|| ||L||. ||swap(L;i;j)|| = ||L||   | [swap_length] |
| 0 | Thm*  k: k: , i,j: , i,j: k. Bij( k. Bij( k; k;  k; (i, j)) k; (i, j)) | [flip_bijection] |
| 5 | Thm*  n,m: n,m: , f:( , f:( n n   m m   ), p:( ), p:( n n   n), q:( n), q:( m m   m). m).
Thm* Bij( n; n;  n; p) n; p)
Thm*  
Thm* Bij( m; m;  m; q) m; q)
Thm*  
Thm* sum(f(p(x),q(y)) | x < n; y < m) = sum(f(x,y) | x < n; y < m) | [permute_double_sum] |
| 2 | Thm*  n,m: n,m: , f,g:( , f,g:( n n   m m   ), d: ), d: . .
Thm* sum(f(x,y)-g(x,y) | x < n; y < m) = d
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = sum(g(x,y) | x < n; y < m)+d | [double_sum_difference] |
| 4 | Thm*  n,m: n,m: , f:( , f:( n n   m m   ), x1,x2: ), x1,x2: n, y1,y2: n, y1,y2: m. m.
Thm*  x1 = x2 x1 = x2 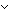  y1 = y2 y1 = y2
Thm*  
Thm* ( x: x: n, y: n, y: m. m.  (x = x1 & y = y1) (x = x1 & y = y1)    (x = x2 & y = y2) (x = x2 & y = y2)   f(x,y) = 0) f(x,y) = 0)
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = f(x1,y1)+f(x2,y2) | [pair_support_double_sum] |
| 1 | Thm*  n,m: n,m: , f,g:( , f,g:( n n   m m   ). ).
Thm* ( x: x: n, y: n, y: m. f(x,y) = g(x,y)) m. f(x,y) = g(x,y))
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = sum(g(x,y) | x < n; y < m) | [double_sum_functionality] |
| 4 | Thm*  L:T List, i,j,x: L:T List, i,j,x: ||L||. swap(L;i;j)[x] = L[((i, j)(x))] ||L||. swap(L;i;j)[x] = L[((i, j)(x))] | [swap_select] |
| 1 | Thm*  k: k: , x,y,i: , x,y,i: k. (y, x)((y, x)(i)) = i k. (y, x)((y, x)(i)) = i | [flip_twice] |