Thm*  k: k: , P:( , P:( k k  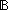 ). ).
Thm* ((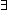 i: i: k. P(i)) k. P(i)) 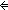  0<search(k;P)) 0<search(k;P))
Thm* & (0<search(k;P)   P(search(k;P)-1) & ( P(search(k;P)-1) & ( j: j: k. j<search(k;P)-1 k. j<search(k;P)-1   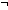 P(j))) P(j))) | [search_property] |
Thm*  k: k: , i,j: , i,j: k. Bij( k. Bij( k; k;  k; (i, j)) k; (i, j)) | [flip_bijection] |
Thm*  k: k: , i,j: , i,j: k. (i, j) = (j, i) k. (i, j) = (j, i) | [flip_symmetry] |
Thm*  n: n: , f:( , f:( n n   ), i: ), i: (n-1). sum(f((i, i+1)(x)) | x < n) = sum(f(x) | x < n) (n-1). sum(f((i, i+1)(x)) | x < n) = sum(f(x) | x < n) | [sum_switch] |
Thm*  f:(T f:(T  T), m:(T T), m:(T   ). ).
Thm* ( x:T. m(f(x)) x:T. m(f(x))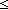 m(x) & (m(f(x)) = m(x) m(x) & (m(f(x)) = m(x)   f(x) = x)) f(x) = x))
Thm*  
Thm* ( x:T. x:T. 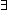 n: n: . f(f^n(x)) = f^n(x)) . f(f^n(x)) = f^n(x)) | [iteration_terminates] |
Thm*  f:(T f:(T  T), n: T), n: , x:T. f(f^n(x)) = f^n+1(x) , x:T. f(f^n(x)) = f^n+1(x) | [fun_exp_add1] |
Thm*  n,m: n,m: , f:(T , f:(T  T). f^n+m = f^n o f^m T). f^n+m = f^n o f^m | [fun_exp_add] |
Thm*  n: n: , h,f:(T , h,f:(T  T). f^n o h = primrec(n;h; T). f^n o h = primrec(n;h;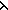 i,g. f o g) i,g. f o g) | [fun_exp_compose] |
Thm*  R:(T R:(T  T T  Prop), n: Prop), n: , x,y:T. (x R^n^-1 y) , x,y:T. (x R^n^-1 y) 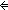  (x R^-1^n y) (x R^-1^n y) | [rel_inverse_exp] |
Thm*  n: n: , T:Type, R1,R2:(T , T:Type, R1,R2:(T  T T  Prop). R1 => R2 Prop). R1 => R2   R1^n => R2^n R1^n => R2^n | [rel_exp_monotone] |
Thm*  R:(T R:(T  T T  Prop), m,n: Prop), m,n: , x,y,z:T. (x R^m y) , x,y,z:T. (x R^m y)   (y R^n z) (y R^n z)   (x R^m+n z) (x R^m+n z) | [rel_exp_add] |
Thm*  k,n: k,n: , R:( , R:( n n   n n  Prop). ( Prop). ( i,j: i,j: n. Dec(i R j)) n. Dec(i R j))   ( ( i,j: i,j: n. Dec(i R^k j)) n. Dec(i R^k j)) | [decidable__rel_exp] |
Thm*  n: n: , T:Type, R:(T , T:Type, R:(T  T T  Prop). R^n Prop). R^n  T T  T T  Prop Prop | [rel_exp_wf] |
Thm*  n,m: n,m: , f,g:( , f,g:( n n   m m   ). ).
Thm* ( x: x: n, y: n, y: m. f(x,y) = g(x,y)) m. f(x,y) = g(x,y))
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = sum(g(x,y) | x < n; y < m) | [double_sum_functionality] |
Thm*  n,m: n,m: , f,g:( , f,g:( n n   m m   ), d: ), d: . .
Thm* sum(f(x,y)-g(x,y) | x < n; y < m) = d
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = sum(g(x,y) | x < n; y < m)+d | [double_sum_difference] |
Thm*  n,m: n,m: , f:( , f:( n n   m m   ), x1,x2: ), x1,x2: n, y1,y2: n, y1,y2: m. m.
Thm* 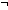 x1 = x2 x1 = x2 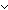 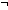 y1 = y2 y1 = y2
Thm*  
Thm* ( x: x: n, y: n, y: m. m. 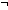 (x = x1 & y = y1) (x = x1 & y = y1)   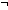 (x = x2 & y = y2) (x = x2 & y = y2)   f(x,y) = 0) f(x,y) = 0)
Thm*  
Thm* sum(f(x,y) | x < n; y < m) = f(x1,y1)+f(x2,y2) | [pair_support_double_sum] |
Thm*  n: n: , f:( , f:( n n   ), m: ), m: (n+1). (n+1).
Thm* sum(f(x) | x < n) = sum(f(x) | x < m)+sum(f(x+m) | x < n-m) | [sum_split] |
Thm*  n: n: , f:( , f:( n n   ), m,k: ), m,k: n. n.
Thm* 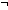 m = k m = k
Thm*  
Thm* ( x: x: n. n. 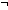 x = m x = m   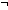 x = k x = k   f(x) = 0) f(x) = 0)   sum(f(x) | x < n) = f(m)+f(k) sum(f(x) | x < n) = f(m)+f(k) | [pair_support] |
Thm*  n,m: n,m: , f:( , f:( n n   m). Inj( m). Inj( n; n;  m; f) m; f)   n n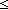 m m | [pigeon-hole] |
Thm*  n,k: n,k: , c:( , c:( n n   k). k).
Thm* 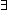 p:( p:( k k  ( ( List)). List)).
Thm* sum(||p(j)|| | j < k) = n
Thm* & ( j: j: k, x,y: k, x,y: ||p(j)||. x<y ||p(j)||. x<y   (p(j))[x]>(p(j))[y]) (p(j))[x]>(p(j))[y])
Thm* & ( j: j: k, x: k, x: ||p(j)||. (p(j))[x]<n & c((p(j))[x]) = j) ||p(j)||. (p(j))[x]<n & c((p(j))[x]) = j) | [finite-partition] |
Thm*  n: n: , f:( , f:( n n   ), m: ), m: n. n.
Thm* ( x: x: n. n. 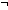 x = m x = m   f(x) = 0) f(x) = 0)   sum(f(x) | x < n) = f(m) sum(f(x) | x < n) = f(m) | [singleton_support_sum] |
Thm*  n: n: , f:( , f:( n n   ). ( ). ( x: x: n. f(x) = 0) n. f(x) = 0)   sum(f(x) | x < n) = 0 sum(f(x) | x < n) = 0 | [empty_support] |
Thm*  n: n: , f:( , f:( n n   ), m: ), m: n. n.
Thm* sum(f(x) | x < n) = f(m)+sum(if x=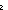 m m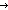 0 else f(x) fi | x < n) 0 else f(x) fi | x < n) | [isolate_summand] |
Thm*  k: k: , f,g:( , f,g:( k k   ), p:( ), p:( k k  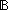 ). ).
Thm* sum(if p(i)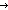 f(i)+g(i) else f(i) fi | i < k) f(i)+g(i) else f(i) fi | i < k)
Thm* =
Thm* sum(f(i) | i < k)+sum(if p(i)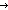 g(i) else 0 fi | i < k) g(i) else 0 fi | i < k) | [sum-ite] |
Thm*  k,b: k,b: , f:( , f:( k k   ). ( ). ( x: x: k. b k. b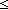 f(x)) f(x))   b b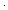 k k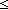 sum(f(x) | x < k) sum(f(x) | x < k) | [sum_lower_bound] |
Thm*  k,b: k,b: , f:( , f:( k k   ). ( ). ( x: x: k. f(x) k. f(x)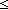 b) b)   sum(f(x) | x < k) sum(f(x) | x < k)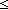 b b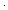 k k | [sum_bound] |
Thm*  k: k: , f,g:( , f,g:( k k   ). ).
Thm* ( x: x: k. f(x) k. f(x)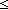 g(x)) g(x))   sum(f(x) | x < k) sum(f(x) | x < k)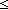 sum(g(x) | x < k) sum(g(x) | x < k) | [sum_le] |
Thm*  n: n: , f,g:( , f,g:( n n   ), d: ), d: . .
Thm* sum(f(x)-g(x) | x < n) = d   sum(f(x) | x < n) = sum(g(x) | x < n)+d sum(f(x) | x < n) = sum(g(x) | x < n)+d | [sum_difference] |
Thm*  n: n: , f,g:( , f,g:( n n   ). ).
Thm* ( i: i: n. f(i) = g(i)) n. f(i) = g(i))   sum(f(x) | x < n) = sum(g(x) | x < n) sum(f(x) | x < n) = sum(g(x) | x < n) | [sum_functionality] |
Thm*  n: n: , a: , a: . sum(a | x < n) = a . sum(a | x < n) = a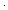 n n | [sum_constant] |
Thm*  n: n: , f,g:( , f,g:( n n   ). ).
Thm* sum(f(x) | x < n)+sum(g(x) | x < n) = sum(f(x)+g(x) | x < n) | [sum_linear] |
Thm*  n: n: , f:( , f:( n n   ). ( ). ( x: x: n. 0 n. 0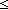 f(x)) f(x))   0 0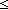 sum(f(x) | x < n) sum(f(x) | x < n) | [non_neg_sum] |
Thm*  m: m: , P:( , P:( m m  Prop). Prop).
Thm* ( i: i: m. Dec(P(i))) m. Dec(P(i)))
Thm*  
Thm* (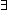 n,k: n,k: , f:( , f:( n n   m), g:( m), g:( k k   m). m).
Thm* (increasing(f;n)
Thm* (& increasing(g;k)
Thm* (& ( i: i: n. P(f(i))) n. P(f(i)))
Thm* (& ( j: j: k. k. 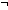 P(g(j))) P(g(j)))
Thm* (& ( i: i: m. ( m. (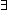 j: j: n. i = f(j)) n. i = f(j)) 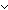 ( (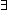 j: j: k. i = g(j)))) k. i = g(j)))) | [increasing_split] |
Thm*  n,m: n,m: , f:( , f:( n n   m), x: m), x: m. f[n:=x] m. f[n:=x]   (n+1) (n+1)   m m | [fappend_wf] |
Thm*  n: n: , f,g:( , f,g:( n n   ). ).
Thm* increasing(f;n)   nondecreasing(g;n) nondecreasing(g;n)   increasing(fadd(f;g);n) increasing(fadd(f;g);n) | [fadd_increasing] |
Thm*  k: k: , x: , x: . nondecreasing( . nondecreasing(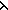 i.x;k) i.x;k) | [const_nondecreasing] |
Thm*  n,m: n,m: , b:T, c:( , b:T, c:( (n+m) (n+m)  T T  T). T).
Thm* primrec(n+m;b;c) = primrec(n;primrec(m;b;c);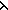 i,t. c(i+m,t)) i,t. c(i+m,t)) | [primrec_add] |
Thm*  T:Type, n: T:Type, n: , b:T, c:( , b:T, c:( n n  T T  T). primrec(n;b;c) T). primrec(n;b;c)  T T | [primrec_wf] |
Thm*  k: k: , f:( , f:( k k   k). k).
Thm* 0<k
Thm*  
Thm* Bij( k; k;  k; f) k; f)
Thm*  
Thm* f(k-1) = k-1   f f   (k-1) (k-1)   (k-1) & Bij( (k-1) & Bij( (k-1); (k-1);  (k-1); f) (k-1); f) | [bijection_restriction] |
Thm*  m,n,k: m,n,k: , f:( , f:( n n   m), g:( m), g:( k k   m). m).
Thm* increasing(f;n)
Thm*  
Thm* increasing(g;k)
Thm*  
Thm* ( i: i: m. ( m. (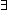 j: j: n. i = f(j)) n. i = f(j)) 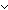 ( (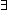 j: j: k. i = g(j))) k. i = g(j)))
Thm*  
Thm* ( j1: j1: n, j2: n, j2: k. k. 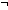 f(j1) = g(j2)) f(j1) = g(j2))   m = n+k m = n+k   | [disjoint_increasing_onto] |
Thm*  k,m: k,m: . ( . (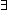 f:( f:( k k   m). Inj( m). Inj( k; k;  m; f)) m; f))   k k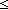 m m | [injection_le] |
Thm*  k: k: , f:( , f:( k k   ), x: ), x: k. increasing(f;k) k. increasing(f;k)   f(0)+x f(0)+x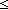 f(x) f(x) | [increasing_lower_bound] |
Thm*  k: k: , f:( , f:( k k   k). increasing(f;k) k). increasing(f;k)   ( ( i: i: k. f(i) = i) k. f(i) = i) | [increasing_is_id] |
Thm*  k,m: k,m: . ( . (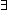 f:( f:( k k   m). increasing(f;k)) m). increasing(f;k))   k k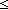 m m | [increasing_le] |
Thm*  k,m: k,m: , f:( , f:( k k   m). increasing(f;k) m). increasing(f;k)   Inj( Inj( k; k;  m; f) m; f) | [increasing_inj] |
Thm*  k,m: k,m: , f:( , f:( k k   m), g:( m), g:( m m   ). ).
Thm* increasing(f;k)   increasing(g;m) increasing(g;m)   increasing(g o f;k) increasing(g o f;k) | [compose_increasing] |
Thm*  k: k: , f:( , f:( k k   ). increasing(f;k) ). increasing(f;k)   ( ( x,y: x,y: k. x<y k. x<y   f(x)<f(y)) f(x)<f(y)) | [increasing_implies] |
Thm*  k: k: . increasing( . increasing(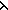 i.i;k) i.i;k) | [id_increasing] |
Def (R^*)(x,y) == 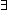 n: n: . x R^n y . x R^n y | [rel_star] |