Thm*  M:sm{i:l}(), I:(M.state M:sm{i:l}(), I:(M.state 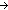 (M.action List) (M.action List) 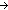 Prop).
( Prop).
( x:M.state. M.init(x) x:M.state. M.init(x) 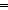 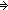 I(x,nil)) I(x,nil)) 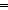 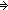 (
( s0,x:M.state, act:M.action, x':M.state, l:M.action List.
M.init(s0) s0,x:M.state, act:M.action, x':M.state, l:M.action List.
M.init(s0) 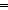 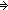 trace_reachable(M;s0;l;x) trace_reachable(M;s0;l;x) 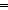 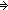 I(x,l) I(x,l) 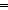 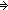 M.trans(x,act,x') M.trans(x,act,x') 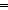 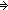 I(x',l @ [act])) I(x',l @ [act]))
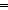 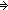 (M |= always s,t.I(s,t))
(M |= always s,t.I(s,t)) | [trace_inv_induction] |
Thm*  M:sm{i:l}(), a:M.action, s,s':M.state.
trace_reachable(M;s;[a];s') M:sm{i:l}(), a:M.action, s,s':M.state.
trace_reachable(M;s;[a];s') 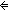 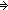 M.trans(s,a,s') M.trans(s,a,s') | [trace_reachable_one] |
Def (M |= x,x',tr,tr'.R(x;x';tr;tr'))
==  x,x':M.state, tr:M.action List, a:M.action.
(M -tr- > x) x,x':M.state, tr:M.action List, a:M.action.
(M -tr- > x) 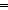 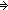 M.trans(x,a,x') M.trans(x,a,x') 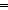 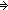 R(x;x';tr;tr @ [a]) R(x;x';tr;tr @ [a]) | [tla] |
Def trace_reachable(M;s;l;s')
== Case of l
nil 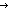 s = s' s = s' 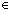 M.state
a.l' M.state
a.l' 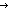 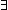 x:M.state. M.trans(s,a,x) & trace_reachable(M;x;l';s')
(recursive) x:M.state. M.trans(s,a,x) & trace_reachable(M;x;l';s')
(recursive) | [trace_reachable] |
Def (f o M)
== mk_sm(M.da o f, M.ds, M.init, 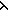 s1,a,s2. s1,a,s2. 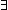 l:Label. kind(a) = f(l) & M.trans(s1, < l,value(a) > ,s2)) l:Label. kind(a) = f(l) & M.trans(s1, < l,value(a) > ,s2)) | [sm_a_rename] |
Def 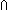 i:I
M(i)
== mk_sm(M(i).da for i i:I
M(i)
== mk_sm(M(i).da for i 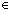 I,
M(i).ds for i I,
M(i).ds for i 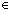 I, I,
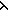 s. s. i:I. M(i).init(s), i:I. M(i).init(s),
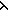 s1,a,s2. s1,a,s2.  i:I. M(i).trans(s1,a,s2)) i:I. M(i).trans(s1,a,s2)) | [sm_all] |