Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( x,y: x,y: . (a . (a x+b x+b y) ~ 1) y) ~ 1) | [coprime_bezout_id0] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   (gcd(a;b) ~ 1) (gcd(a;b) ~ 1) | [coprime_elim_a] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( c: c: . c | a . c | a   c | b c | b   (c ~ 1)) (c ~ 1)) | [coprime_elim] |
Thm*  p: p: . prime(p) . prime(p)    p = 0 & p = 0 &  (p ~ 1) & ( (p ~ 1) & ( a: a: . a | p . a | p   (a ~ 1) (a ~ 1) 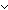 (a ~ p)) (a ~ p)) | [prime_elim] |
Thm*  a: a:  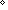 , b: , b: . a . a b | a b | a   (b ~ 1) (b ~ 1) | [self_divisor_mul] |
Thm*  a: a: . atomic(a) . atomic(a)    (a ~ 1) & ( (a ~ 1) & ( b: b: . b | a . b | a   (b ~ 1) (b ~ 1) 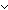 (b ~ a)) (b ~ a)) | [atomic_char] |
Thm*  a,b,c: a,b,c: . gcd(gcd(a;b);c) ~ gcd(a;gcd(b;c)) . gcd(gcd(a;b);c) ~ gcd(a;gcd(b;c)) | [gcd_assoc] |
Thm*  a,b,n: a,b,n: . (n . (n gcd(a;b)) ~ gcd(n gcd(a;b)) ~ gcd(n a;n a;n b) b) | [gcd_mul] |
Thm*  a,b: a,b: . gcd(a;b) ~ gcd(b;a) . gcd(a;b) ~ gcd(b;a) | [gcd_sym] |
Thm*  a,b,y1,y2: a,b,y1,y2: . GCD(a;b;y1) . GCD(a;b;y1)   GCD(a;b;y2) GCD(a;b;y2)   (y1 ~ y2) (y1 ~ y2) | [gcd_unique] |
Thm*  a,a',b,b',y,y': a,a',b,b',y,y': . .
Thm* (a ~ a')   (b ~ b') (b ~ b')   (y ~ y') (y ~ y')   (GCD(a;b;y) (GCD(a;b;y)   GCD(a';b';y')) GCD(a';b';y')) | [gcd_p_functionality_wrt_assoced] |
Thm*  a,b: a,b: . (a ~ b) . (a ~ b)   a = b a = b | [assoced_nelim] |
Thm*  a: a: . a | 1 . a | 1   (a ~ 1) (a ~ 1) | [unit_chars] |
Thm*  a: a: . |a| ~ a . |a| ~ a | [absval_assoced] |
Thm*  a: a: . (-a) ~ a . (-a) ~ a | [neg_assoced] |
Thm*  a,b: a,b: , n: , n:  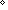 . ((n . ((n a) ~ (n a) ~ (n b)) b))   (a ~ b) (a ~ b) | [mul_cancel_in_assoced] |
Thm*  a,b: a,b: . (a ~ b) . (a ~ b)   a = b a = b 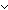 a = -b a = -b | [assoced_elim] |
Thm*  a,b,a',b': a,b,a',b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   ((a ~ b) ((a ~ b)   (a' ~ b')) (a' ~ b')) | [assoced_functionality_wrt_assoced] |
Thm*  a,a',b,b': a,a',b,b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   ((a ((a b) ~ (a' b) ~ (a' b')) b')) | [multiply_functionality_wrt_assoced] |
Thm*  a,b,c: a,b,c: . (a ~ b) . (a ~ b)   (b ~ c) (b ~ c)   (a ~ c) (a ~ c) | [assoced_transitivity] |
Thm*  a,b: a,b: . a = b . a = b   (a ~ b) (a ~ b) | [assoced_weakening] |
Thm*  a,a',b,b': a,a',b,b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   (a | b (a | b   a' | b') a' | b') | [divides_functionality_wrt_assoced] |
Thm* EquivRel x,y: . x ~ y . x ~ y | [assoced_equiv_rel] |
Def prime(a) ==  a = 0 & a = 0 &  (a ~ 1) & ( (a ~ 1) & ( b,c: b,c: . a | b . a | b c c   a | b a | b 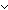 a | c) a | c) | [prime] |
Def atomic(a) ==  a = 0 & a = 0 &  (a ~ 1) & (a ~ 1) &  reducible(a) reducible(a) | [atomic] |
Def reducible(a) ==  b,c: b,c:  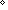 . .  (b ~ 1) & (b ~ 1) &  (c ~ 1) & a = b (c ~ 1) & a = b c c | [reducible] |