is mentioned by

Thm* r:, s:{s':| CoPrime(r,s') }, a,b:. Thm* 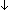x:. ((x = a mod r) & (x = b mod s))	[chrem_exists_a]
Thm* r,s:. CoPrime(r,s)  (a,b:. x:. (x = a mod r) & (x = b mod s))	[chrem_exists]
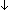Thm* r:, s:{s':| CoPrime(r,s') }. x:. ((x = 1 mod r) & (x = 0 mod s))	[chrem_exists_aux_a]
Thm* r,s:. CoPrime(r,s)  (x:. (x = 1 mod r) & (x = 0 mod s))	[chrem_exists_aux]
Thm* m,a,a',b,b':. (a = a' mod m)  (b = b' mod m)  ((ab) = (a'b') mod m)	[multiply_functionality_wrt_eqmod]
Thm* m,a,a',b,b':. (a = a' mod m)  (b = b' mod m)  ((a+b) = (a'+b') mod m)	[add_functionality_wrt_eqmod]
Thm* m,a,a',b,b':. Thm* (a = a' mod m)  (b = b' mod m)  ((a = b mod m)  (a' = b' mod m))	[eqmod_fun]
Thm* m,m',a,a',b,b':. Thm* m = m' Thm*  Thm* (a = a' mod m)  (b = b' mod m)  ((a = b mod m)  (a' = b' mod m'))	[eqmod_functionality_wrt_eqmod]
Thm* m,a,b:. (a = b mod m)  (b = a mod m)	[eqmod_inversion]
Thm* m,a,b,c:. (a = b mod m)  (b = c mod m)  (a = c mod m)	[eqmod_transitivity]
Thm* m,a,b:. a = b  (a = b mod m)	[eqmod_weakening]

Try larger context: StandardLIB IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html