Def GCD(a;b;y) == y | a & y | b & (z:. z | a & z | b  z | y)

is mentioned by

Thm* a,b,y,n:. GCD(a;b;y)  GCD(na;nb;ny)	[gcd_p_mul]
Thm* a,b:. u,v:. GCD(a;b;ua+vb)	[bezout_ident]
Thm* b:, a:. u,v:. GCD(a;b;ua+vb)	[bezout_ident_n]
Thm* a,b:. y:. GCD(a;b;y)	[gcd_exists]
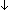Thm* b:, a:. y:. GCD(a;b;y)	[gcd_ex_n]
Thm* b:, a:. y:. GCD(a;b;y)	[gcd_exists_n]
Thm* a,b:. y:. GCD(a;b;y) & gcd(a;b) = y	[gcd_elim]
Thm* a,b:. GCD(a;b;gcd(a;b))	[gcd_sat_pred]
Thm* a,b:. GCD(a;b;gcd(a;b))	[gcd_sat_gcd_p]
Thm* a,b,c,x,y:. Thm* GCD(a;b;x) Thm*  Thm* GCD(x;c;y) Thm*  Thm* y | a & y | b & y | c & (z:. z | a  z | b  z | c  z | y)	[gcd_of_triple]
Thm* a,b,y1,y2:. GCD(a;b;y1)  GCD(a;b;y2)  (y1 ~ y2)	[gcd_unique]
Thm* a,b,y,k:. GCD(a;b;y)  GCD(a;b+ka;y)	[gcd_p_shift]
Thm* a,b,y:. GCD(a;b;y)  GCD(a;-b;y)	[gcd_p_neg_arg_2]
Thm* a,b,y:. GCD(a;b;y)  GCD(-a;b;y)	[gcd_p_neg_arg_a]
Thm* a,b,y:. GCD(a;b;y)  GCD(a;-b;y)	[gcd_p_neg_arg]
Thm* a,b,y:. GCD(a;b;y)  GCD(b;a;y)	[gcd_p_sym_a]
Thm* a,b,y:. GCD(a;b;y)  GCD(b;a;y)	[gcd_p_sym]
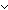Thm* a,b:. GCD(a;0;b)  a = b  a = -b	[gcd_p_zero_rel]
Thm* a:. GCD(a;1;1)	[gcd_p_one]
Thm* a:. GCD(a;0;a)	[gcd_p_zero]
Thm* a:. GCD(a;a;a)	[gcd_p_eq_args]
Thm* a,a',b,b',y,y':. Thm* (a ~ a')  (b ~ b')  (y ~ y')  (GCD(a;b;y)  GCD(a';b';y'))	[gcd_p_functionality_wrt_assoced]
Def CoPrime(a,b) == GCD(a;b;1)	[coprime]

Try larger context: StandardLIB IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html