Selected Objects
| THM | incl_aux2_quo |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop).
(EquivRel x,y: Prop).
(EquivRel x,y: n. x E y) n. x E y)   ( ( z:x,y: z:x,y: m//(x E y). z m//(x E y). z 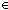 x,y: x,y: n//(x E y)) n//(x E y)) |
| THM | incl_aux3_quo |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop).
(EquivRel i,j: Prop).
(EquivRel i,j: n. i E j) n. i E j)   ( ( x,y:i,j: x,y:i,j: m//(i E j). x = y m//(i E j). x = y 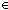 i,j: i,j: n//(i E j) n//(i E j)   x = y) x = y) |
| THM | incl_aux4_quo |  n:{1...}, E:( n:{1...}, E:( n n   n n  Prop).
(EquivRel i,j: Prop).
(EquivRel i,j: n. i E j) n. i E j)   (
( x:i,j: x:i,j: n//(i E j). n//(i E j).  x = n-1 x = n-1 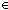 i,j: i,j: n//(i E j) n//(i E j)   x x 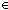 i,j: i,j: (n-1)//(i E j)) (n-1)//(i E j)) |
| THM | incl_aux5_quo |  E:(T E:(T  T T  Prop). (EquivRel x,y:T. x E y) Prop). (EquivRel x,y:T. x E y)   ( ( x,y:T. x = y x,y:T. x = y   x = y x = y 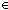 u,v:T//(u E v)) u,v:T//(u E v)) |
| THM | incl_aux6_quo |  R:(T R:(T  T T  Prop).
(EquivRel x,y:T. x R y) Prop).
(EquivRel x,y:T. x R y)   (
( Q:((x,y:T//(x R y)) Q:((x,y:T//(x R y))  (x,y:T//(x R y)) (x,y:T//(x R y))  Prop).
(EquivRel u,v:x,y:T//(x R y). u Q v) Prop).
(EquivRel u,v:x,y:T//(x R y). u Q v)   (EquivRel x,y:T. x Q y)) (EquivRel x,y:T. x Q y)) |
| THM | rest_refl_rel |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop). Refl( Prop). Refl( n;x,y.x E y) n;x,y.x E y)   Refl( Refl( m;x,y.x E y) m;x,y.x E y) |
| THM | rest_symm_rel |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop). Sym x,y: Prop). Sym x,y: n. x E y n. x E y   Sym x,y: Sym x,y: m. x E y m. x E y |
| THM | rest_tran_rel |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop). Trans x,y: Prop). Trans x,y: n. x E y n. x E y   Trans x,y: Trans x,y: m. x E y m. x E y |
| THM | rest_equi_rel |  n:{1...}, m: n:{1...}, m: n, E:( n, E:( n n   n n  Prop). (EquivRel x,y: Prop). (EquivRel x,y: n. x E y) n. x E y)   (EquivRel x,y: (EquivRel x,y: m. x E y) m. x E y) |
| THM | quotient_of_nsubn |  n:{1...}, E:( n:{1...}, E:( n n   n n  Prop).
(EquivRel x,y: Prop).
(EquivRel x,y: n. x E y) & ( n. x E y) & ( x,y: x,y: n. Dec(x E y)) n. Dec(x E y))   ( (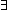 m: m: (n+1). (n+1).  m ~ (i,j: m ~ (i,j: n//(i E j))) n//(i E j))) |
| THM | quo_of_quo |  R:(T R:(T  T T  Prop).
(EquivRel x,y:T. x R y) Prop).
(EquivRel x,y:T. x R y)   (
( Q:((x,y:T//(x R y)) Q:((x,y:T//(x R y))  (x,y:T//(x R y)) (x,y:T//(x R y))  Prop).
(EquivRel u,v:x,y:T//(x R y). u Q v) Prop).
(EquivRel u,v:x,y:T//(x R y). u Q v)   ((x,y:T//(x Q y)) ~ (u,v:(x,y:T//(x R y))//(u Q v)))) ((x,y:T//(x Q y)) ~ (u,v:(x,y:T//(x R y))//(u Q v)))) |
| def | preima_of_rel | R_f(x,y) == (f(x)) R (f(y)) |
| THM | preima_of_equiv_rel |  f:(A f:(A  B), R:(B B), R:(B  B B  Prop). (EquivRel x,y:B. x R y) Prop). (EquivRel x,y:B. x R y)   (EquivRel x,y:A. x R_f y) (EquivRel x,y:A. x R_f y) |
| THM | one_one_corr_refl | A ~ A |
| THM | one_one_corr_symm | (A ~ B)   (B ~ A) (B ~ A) |
| THM | one_one_corr_tran | (A ~ B)   (B ~ C) (B ~ C)   (A ~ C) (A ~ C) |
| THM | quotient_1_1_corr |  f:(A f:(A  B), R:(B B), R:(B  B B  Prop).
Bij(A; B; f) Prop).
Bij(A; B; f)   (EquivRel x,y:B. x R y)
(EquivRel x,y:B. x R y)   (
(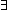 F:((x,y:A//(x R_f y)) F:((x,y:A//(x R_f y))  (x,y:B//(x R y))). Bij(x,y:A//(x R_f y); x,y:B//(x R y); F)) (x,y:B//(x R y))). Bij(x,y:A//(x R_f y); x,y:B//(x R y); F)) |
| THM | quotient_of_finite |  n:{1...}, A:Type, R:(A n:{1...}, A:Type, R:(A  A A  Prop).
( Prop).
( n ~ A) n ~ A)   (EquivRel x,y:A. x R y) (EquivRel x,y:A. x R y)   ( ( x,y:A. Dec(x R y)) x,y:A. Dec(x R y))   ( (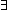 m: m: (n+1). (n+1).  m ~ (x,y:A//(x R y))) m ~ (x,y:A//(x R y))) |