| 1 | 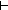  A,B:Type, f:(A A,B:Type, f:(A  B), R:(B B), R:(B  B B  Prop).
( Prop).
( a:B. a R a) & ( a:B. a R a) & ( a,b:B. (a R b) a,b:B. (a R b)   (b R a)) & ( (b R a)) & ( a,b,c:B. (a R b) a,b,c:B. (a R b)   (b R c) (b R c)   (a R c)) (a R c))   (
( a:A. a ( a:A. a (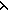 x,y. (f(x)) R (f(y))) a)
& ( x,y. (f(x)) R (f(y))) a)
& ( a,b:A. (a ( a,b:A. (a (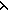 x,y. (f(x)) R (f(y))) b) x,y. (f(x)) R (f(y))) b)   (b ( (b (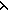 x,y. (f(x)) R (f(y))) a))
& ( x,y. (f(x)) R (f(y))) a))
& ( a,b,c:A.
(a ( a,b,c:A.
(a (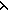 x,y. (f(x)) R (f(y))) b) x,y. (f(x)) R (f(y))) b)   (b ( (b (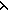 x,y. (f(x)) R (f(y))) c) x,y. (f(x)) R (f(y))) c)   (a ( (a (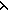 x,y. (f(x)) R (f(y))) c)) x,y. (f(x)) R (f(y))) c)) |