Selected Objects
| COM | sqequal_com |
Here are the essentials:
... |
| COM | sq_type_com |
There are other types in Nuprl that we can consider first order types.
... |
| def | sq_type |
SQType(T) ==  x,y:T. x = y x,y:T. x = y 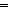 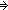 {x ~ y} {x ~ y} |
| THM | int_sq |
SQType(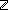 ) ) |
| THM | nat_sq |
SQType(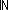 ) ) |
| THM | bool_sq |
SQType(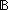 ) ) |
| THM | atom_sq |
SQType(Atom) |
| THM | bool_sim_true |
 b: b: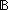 . b = true . b = true 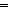 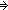 (b ~ true (b ~ true ) ) |
| THM | bool_sim_false |
 b: b: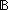 . b = false . b = false 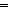 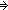 (b ~ false (b ~ false ) ) |
| THM | eq_int_eq_true_intro |
 i,j: i,j: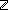 . i = j . i = j 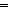 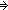 ((i= ((i= j) ~ true j) ~ true ) ) |
| THM | eq_int_eq_false_intro |
 i,j: i,j: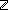 . . 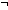 i = j i = j 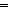 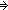 ((i= ((i= j) ~ false j) ~ false ) ) |
| THM | lt_int_eq_true_elim |
 i,j: i,j: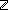 . (i< . (i< j) = true j) = true 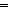 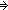 i<j i<j |
| THM | lt_int_eq_false_elim |
 i,j: i,j: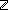 . (i< . (i< j) = false j) = false 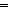 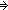 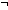 i<j i<j |
| THM | eq_atom_eq_true_elim |
 x,y:Atom. x= x,y:Atom. x= y y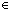 Atom = true Atom = true 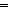 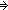 x = y x = y |
| THM | eq_atom_eq_false_elim |
 x,y:Atom. x= x,y:Atom. x= y y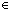 Atom = false Atom = false 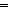 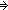 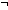 x = y x = y |
| THM | eq_int_eq_true_elim_sqequal |
 i,j: i,j: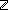 . ((i= . ((i= j) ~ true j) ~ true ) ) 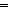 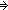 i = j i = j |
| THM | eq_int_eq_false_elim_sqequal |
 i,j: i,j: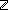 . ((i= . ((i= j) ~ false j) ~ false ) ) 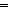 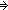 i i 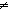 j j |
| THM | lt_int_eq_true_elim_sqequal |
 i,j: i,j: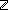 . ((i< . ((i< j) ~ true j) ~ true ) ) 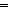 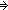 i<j i<j |
| THM | lt_int_eq_false_elim_sqequal |
 i,j: i,j: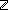 . ((i< . ((i< j) ~ false j) ~ false ) ) 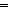 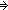 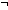 i<j i<j |
| THM | eq_atom_eq_true_elim_sqequal |
 x,y:Atom. (x= x,y:Atom. (x= y y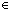 Atom ~ true Atom ~ true ) ) 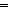 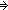 x = y x = y |
| THM | eq_atom_eq_false_elim_sqequal |
 x,y:Atom. (x= x,y:Atom. (x= y y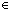 Atom ~ false Atom ~ false ) ) 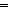 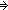 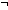 x = y x = y |
| THM | bool_cases_sqequal |
 b: b: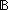 . (b ~ true . (b ~ true ) ) 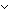 (b ~ false (b ~ false ) ) |