---

Step * 1 of Lemma aa_bst_insert_trial4


1. t : aa_ltree()@i
2. i : @i
3. aa_binary_search_tree(t)@i
 tp:aa_ltree()
   (aa_binary_search_tree(tp)  (j:. (aa_bst_member_prop(j;tp)  (j = i) 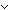 aa_bst_member_prop(j;t))))
BY
{ (InstLemma `aa_ltree-induction` [; 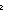t.aa_binary_search_tree(t)
                                          (tp:aa_ltree()
                                              (aa_binary_search_tree(tp)
                                               (j:
                                                   (aa_bst_member_prop(j;tp)  (j = i) 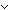 aa_bst_member_prop(j;t)))))
   ] THEN Auto
   THEN Try (Complete ((BackThruSomeHyp THEN Auto)))
   ) }

1
1. t : aa_ltree()@i
2. i : @i
3. aa_binary_search_tree(t)@i
4. aa_binary_search_tree(aa_lt_leaf())@i
 tp:aa_ltree()
   (aa_binary_search_tree(tp)  (j:. (aa_bst_member_prop(j;tp)  (j = i) 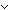 aa_bst_member_prop(j;aa_lt_leaf()))))

2
1. t : aa_ltree()@i
2. i : @i
3. aa_binary_search_tree(t)@i
4. val : @i
5. left_subtree : aa_ltree()@i
6. right_subtree : aa_ltree()@i
7. aa_binary_search_tree(left_subtree)
 (tp:aa_ltree()
     (aa_binary_search_tree(tp)
      (j:. (aa_bst_member_prop(j;tp)  (j = i) 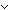 aa_bst_member_prop(j;left_subtree)))))@i
8. aa_binary_search_tree(right_subtree)
 (tp:aa_ltree()
     (aa_binary_search_tree(tp)
      (j:. (aa_bst_member_prop(j;tp)  (j = i) 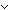 aa_bst_member_prop(j;right_subtree)))))@i
9. aa_binary_search_tree(aa_lt_node(val;left_subtree;right_subtree))@i
 tp:aa_ltree()
   (aa_binary_search_tree(tp)
    (j:. (aa_bst_member_prop(j;tp)  (j = i) 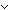 aa_bst_member_prop(j;aa_lt_node(val;left_subtree;right_subtree)))))



1.  t  :  aa\_ltree(\mBbbZ{})@i
2.  i  :  \mBbbZ{}@i
3.  aa\_binary\_search\_tree(t)@i
\mvdash{}  \mexists{}tp:aa\_ltree(\mBbbZ{})
      (aa\_binary\_search\_tree(tp)
      \mwedge{}  (\mforall{}j:\mBbbZ{}.  (aa\_bst\_member\_prop(j;tp)  \mLeftarrow{}{}\mRightarrow{}  (j  =  i)  \mvee{}  aa\_bst\_member\_prop(j;t))))


By

(InstLemma  `aa\_ltree-induction`  [\mkleeneopen{}\mBbbZ{}\mkleeneclose{};  \mkleeneopen{}\mlambda{}\msubtwo{}t.aa\_binary\_search\_tree(t)
                                                                              {}\mRightarrow{}  (\mexists{}tp:aa\_ltree(\mBbbZ{})
                                                                                        (aa\_binary\_search\_tree(tp)
                                                                                        \mwedge{}  (\mforall{}j:\mBbbZ{}
                                                                                                  (aa\_bst\_member\_prop(j;tp)
                                                                                                  \mLeftarrow{}{}\mRightarrow{}  (j  =  i)  \mvee{}  aa\_bst\_member\_prop(j;t)))))\mkleeneclose{}
  ]  THEN  Auto\mcdot{}
  THEN  Try  (Complete  ((BackThruSomeHyp  THEN  Auto)))
  )



Home Index