Nuprl Lemma : aa_data_wrapper-induction
[T:Type]. [P:aa_data_wrapper(T) 
].
((nd:aa_data_wrapper(T). (P[nd] 
P[aa_data_wrapnode(nd)]))
(val:T. P[aa_data_wrapleaf(val)])
{x:aa_data_wrapper(T). P[x]})
Proof
Definitions occuring in Statement :
aa_data_wrapleaf: aa_data_wrapleaf(val),
aa_data_wrapnode: aa_data_wrapnode(nd),
aa_data_wrapper: aa_data_wrapper(T),
uall: [x:A]. B[x],
prop: ,
guard: {T},
so_apply: x[s],
all: x:A. B[x],
implies: P Q,
function: x:A B[x],
universe: Type
Definitions :
uall: [x:A]. B[x],
prop: ,
implies: P Q,
all: x:A. B[x],
so_apply: x[s],
guard: {T},
type-monotone: Monotone(T.F[T]),
uimplies: b supposing a,
member: t 
T,
so_lambda: 
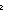x.t[x],
aa_data_wrapper: aa_data_wrapper(T),
aa_data_wrapnode: aa_data_wrapnode(nd),
aa_data_wrapleaf: aa_data_wrapleaf(val)
Lemmas :
subtype_rel_sum,
aa_data_wrapper_wf,
all_wf,
aa_data_wrapleaf_wf,
aa_data_wrapnode_wf
\mforall{}[T:Type]. \mforall{}[P:aa\_data\_wrapper(T) {}\mrightarrow{} \mBbbP{}].
((\mforall{}nd:aa\_data\_wrapper(T). (P[nd] {}\mRightarrow{} P[aa\_data\_wrapnode(nd)]))
{}\mRightarrow{} (\mforall{}val:T. P[aa\_data\_wrapleaf(val)])
{}\mRightarrow{} \{\mforall{}x:aa\_data\_wrapper(T). P[x]\})
Date html generated:
2013_03_20-AM-11_02_33
Last ObjectModification:
2012_11_27-AM-10_33_10
Home
Index