Step
*
1
of Lemma
aa_fib_count_wf
1. n :  @i
@i
2.  n1:
n1: . aa_fib_count(n1)
. aa_fib_count(n1) 

 supposing n1 < n
supposing n1 < n
 aa_fib_count(n)
aa_fib_count(n) 


BY
{ ProveWfLemma }
1
1. n :  @i
@i
2.  n1:
n1: . aa_fib_count(n1)
. aa_fib_count(n1) 

 supposing n1 < n
supposing n1 < n
 fix((
fix(( f,n. if (n =
f,n. if (n = 0)
0) 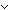
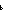 (n =
(n = 1)
1)
then <1, 0>
else <(fst((f (n - 1)))) + (fst((f (n - 2)))), (snd((f (n - 1)))) + (snd((f (n - 2))))>
fi ))
n 

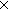

1. n : \mBbbN{}@i
2. \mforall{}n1:\mBbbN{}. aa\_fib\_count(n1) \mmember{} \mBbbN{} \mtimes{} \mBbbN{} supposing n1 < n
\mvdash{} aa\_fib\_count(n) \mmember{} \mBbbN{} \mtimes{} \mBbbN{}
By
ProveWfLemma
Home
Index