---

Step * 1 1 1 of Lemma fin_spr_is_spr


1. B :  List  @i
2. a :  List@i
3. 0 = 0@i
4. (a  fspr(B))
 if (a @ [0]  fspr(B)) then 0 else 1 fi  = 0
BY
{ ((Assert (a @ [0]  fspr(B)) BY RWO "list-in-fin_spr_unfold" 0) THEN Auto) }

1
1. B :  List  @i
2. a :  List@i
3. 0 = 0@i
4. (a  fspr(B))
 if (||a @ [0]|| = 0)
then tt
else (firstn(||a @ [0]|| - 1;a @ [0])  fspr(B))  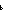last(a @ [0]) z B firstn(||a @ [0]|| - 1;a @ [0])
fi 



1.  B  :  \mBbbN{}  List  {}\mrightarrow{}  \mBbbN{}@i
2.  a  :  \mBbbN{}  List@i
3.  0  =  0@i
4.  \muparrow{}(a  \mmember{}  fspr(B))
\mvdash{}  if  (a  @  [0]  \mmember{}  fspr(B))  then  0  else  1  fi    =  0


By

((Assert  \muparrow{}(a  @  [0]  \mmember{}  fspr(B))  BY  RWO  "list-in-fin\_spr\_unfold"  0)  THEN  Auto)



Home Index