Nuprl Lemma : vr_base4-ext
n:
. 
L:4 List. (n =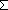 
(4^i * L[i] | i < ||L||))
Proof not projected
Definitions occuring in Statement :
select: l[i],
length: ||as||,
int_seg: {i..j
},
nat: ,
all: x:A. B[x],
exists: x:A. B[x],
list: type List,
multiply: n * m,
natural_number: $n,
int: 
,
equal: s = t,
sum: 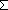(f[x] | x < k),
exp: i^n
Definitions :
tactic: Error :tactic,
lambda: 
x.A[x],
vr_base4,
member: t 
T,
equal: s = t,
ind: ind def,
sqequal: s ~ t,
all: x:A. B[x],
function: x:A 
B[x],
uall: [x:A]. B[x],
isect: 
x:A. B[x],
subtype_rel: A 
r B,
exists: x:A. B[x],
product: x:A 
B[x],
int: ,
list: type List,
int_seg: {i..j},
nat: ,
uimplies: b supposing a,
sq_type: SQType(T),
uiff: uiff(P;Q),
and: P 
Q,
less_than: a < b,
not: 
A,
ge: i 
j ,
le: A 
B,
strong-subtype: strong-subtype(A;B)
Lemmas :
subtype_base_sq,
nat_wf,
int_seg_wf,
vr_base4
\mforall{}n:\mBbbN{}. \mexists{}L:\mBbbN{}4 List. (n = \mSigma{}(4\^{}i * L[i] | i < ||L||))
Date html generated:
2012_02_20-PM-03_31_13
Last ObjectModification:
2012_02_02-PM-01_54_45
Home
Index