{ CountComb() 
CombinatorDef }
{ Proof }
Definitions occuring in Statement :
CountComb: CountComb(),
combinator-def: CombinatorDef,
member: t T
Definitions :
universe: Type,
member: t T,
equal: s = t,
natural_number: $n,
le: A 
B,
prop: 
,
function: x:A 
B[x],
all: 
x:A. B[x],
nat: 
,
int: 
,
add: n + m,
less_than: a < b,
void: Void,
implies: P 
Q,
false: False,
not: 
A,
set: {x:A| B[x]} ,
real: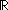 
,
subtype: S 
T,
grp_car: Error :grp_car,
subtype_rel: A r B,
strong-subtype: strong-subtype(A;B),
rationals: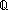 
,
lambda: 
x.A[x],
isect: 
x:A. B[x],
p-outcome: Outcome,
PolyAccumComb: PolyAccumComb(B;f;x),
CountComb: CountComb()
Lemmas :
PolyAccumComb_wf,
nat_wf,
member_wf,
le_wf
CountComb() \mmember{} CombinatorDef
Date html generated:
2010_08_27-PM-08_23_57
Last ObjectModification:
2010_06_23-PM-05_25_32
Home
Index