{ 
s:SES. es:EO+(Info). e:E. a:Atom1.
(e has* a 
(e has a) 
(
z:E. ((z ->> e) 
z has* a))) }
{ Proof }
Definitions occuring in Statement :
event-has*: e has* a,
ses-info-flow: ->>,
event-has: (e has a),
ses-info: Info,
security-event-structure: SES,
event-ordering+: EO+(Info),
es-E: E,
infix_ap: x f y,
all: x:A. B[x],
exists: x:A. B[x],
iff: P Q,
or: P Q,
and: P Q,
atom: Atom$n
Definitions :
product: x:A 
B[x],
infix_ap: x f y,
and: P Q,
es-E: E,
exists: x:A. B[x],
event-has*: e has* a,
union: left + right,
event-has: (e has a),
or: P Q,
equal: s = t,
member: t 
T,
function: x:A 
B[x],
all: x:A. B[x],
security-event-structure: SES,
ses-info: Info,
event-ordering+: EO+(Info),
subtype: S 
T,
event_ordering: EO,
atom: Atom$n,
ses-info-flow: ->>,
apply: f a,
prop: 
,
subtype_rel: A r B,
strong-subtype: strong-subtype(A;B),
record-select: r.x,
dep-isect: Error :dep-isect,
eq_atom: x =a y,
eq_atom: eq_atom$n(x;y),
record+: record+,
implies: P Q,
rev_implies: P Q,
iff: P Q,
nat: 
,
lambda: 
x.A[x],
rel_star: R^*,
rel_exp: R^n,
less_than: a < b,
set: {x:A| B[x]} ,
cand: A c B,
not: 
A,
le: A 
B,
false: False,
int: 
,
natural_number: $n,
subtract: n - m,
universe: Type,
guard: {T},
minus: -n,
add: n + m,
void: Void,
real: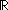 
,
grp_car: |g|,
rationals: 
,
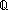Auto: Error :Auto,
CollapseTHEN: Error :CollapseTHEN,
D: Error :D,
limited-type: LimitedType
Lemmas :
rel_star_iff,
rel_star_weakening,
nat_wf,
member_wf,
le_wf,
rel_exp_wf,
rel_star_wf,
rel_exp_iff,
event-has_wf,
ses-info-flow_wf,
event-has*_wf,
es-E_wf,
event-ordering+_inc,
event-ordering+_wf,
ses-info_wf,
security-event-structure_wf
\mforall{}s:SES. \mforall{}es:EO+(Info). \mforall{}e:E. \mforall{}a:Atom1. (e has* a \mLeftarrow{}{}\mRightarrow{} (e has a) \mvee{} (\mexists{}z:E. ((z ->> e) \mwedge{} z has* a)))
Date html generated:
2011_08_17-PM-07_20_46
Last ObjectModification:
2010_09_24-PM-03_13_01
Home
Index