{ 
[B:Type]. [n:
]. [A:n 
Type]. [bags:k:n bag(A k)].
[f:Id funtype(n;A;B)]. [b:B]. [l:Id].
(bag-member(B;b;lifting-loc-gen-rev(n;bags;l;f))
lst:k:n (A k)
(([k:n]. bag-member(A k;lst k;bags k))
((uncurry-rev(n;f l) lst) = b))) }
{ Proof }
Definitions occuring in Statement :
lifting-loc-gen-rev: lifting-loc-gen-rev(n;bags;loc;f),
uncurry-rev: uncurry-rev(n;f),
Id: Id,
int_seg: {i..j
},
nat: ,
uall: [x:A]. B[x],
exists: x:A. B[x],
iff: P Q,
squash: T,
and: P Q,
apply: f a,
function: x:A B[x],
natural_number: $n,
universe: Type,
equal: s = t,
bag-member: bag-member(T;x;bs),
bag: bag(T),
funtype: funtype(n;A;T)
Definitions :
CollapseTHENA: Error :CollapseTHENA,
Auto: Error :Auto,
CollapseTHEN: Error :CollapseTHEN,
apply: f a,
and: P Q,
iff: P Q,
isect: 
x:A. B[x],
uall: [x:A]. B[x],
int_seg: {i..j},
bag: bag(T),
function: x:A B[x],
universe: Type,
set: {x:A| B[x]} ,
squash: T,
implies: P Q,
product: x:A 
B[x],
nat: ,
quotient: x,y:A//B[x; y],
funtype: funtype(n;A;T),
Id: Id,
primrec: primrec(n;b;c),
atom: Atom$n,
member: t 
T,
equal: s = t,
all: x:A. B[x],
natural_number: $n,
int: 
,
subtype: S 
T,
grp_car: |g|,
real: 
,
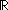lifting-loc-gen-rev: lifting-loc-gen-rev(n;bags;loc;f)
Lemmas :
lifting-member-simple,
nat_wf,
int_seg_wf,
bag_wf,
funtype_wf,
Id_wf
\mforall{}[B:Type]. \mforall{}[n:\mBbbN{}]. \mforall{}[A:\mBbbN{}n {}\mrightarrow{} Type]. \mforall{}[bags:k:\mBbbN{}n {}\mrightarrow{} bag(A k)]. \mforall{}[f:Id {}\mrightarrow{} funtype(n;A;B)]. \mforall{}[b:B].
\mforall{}[l:Id].
(bag-member(B;b;lifting-loc-gen-rev(n;bags;l;f))
\mLeftarrow{}{}\mRightarrow{} \mdownarrow{}\mexists{}lst:k:\mBbbN{}n {}\mrightarrow{} (A k)
((\mforall{}[k:\mBbbN{}n]. bag-member(A k;lst k;bags k)) \mwedge{} ((uncurry-rev(n;f l) lst) = b)))
Date html generated:
2011_08_17-PM-06_07_32
Last ObjectModification:
2011_06_01-PM-01_12_57
Home
Index