{ 
[A:
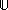']. [dfp1,dfp2:DataflowProgram(A)]. [B:Type].
[G:bag(df-program-type(dfp1)) 
bag(df-program-type(dfp2)) bag(B)].
better-parallel-dataflow(
2;
k.[df-program-meaning(dfp1); df-program-meaning(dfp2)][k];
g.G[g 0;g 1])
= df-program-meaning(parallel-df-prog2(B;G;dfp1;dfp2))
supposing (G[{};{}] = {}) 
valueall-type(B) }
{ Proof }
Definitions occuring in Statement :
parallel-df-prog2: parallel-df-prog2(B;G;dfp1;dfp2),
df-program-meaning: df-program-meaning(dfp),
df-program-type: df-program-type(dfp),
dataflow-program: DataflowProgram(A),
better-parallel-dataflow: better-parallel-dataflow,
dataflow: dataflow(A;B),
select: l[i],
uimplies: b supposing a,
uall: [x:A]. B[x],
so_apply: x[s1;s2],
and: P Q,
apply: f a,
lambda: x.A[x],
function: x:A B[x],
cons: [car / cdr],
nil: [],
natural_number: $n,
universe: Type,
equal: s = t,
empty-bag: {},
bag: bag(T),
valueall-type: valueall-type(T)
Definitions :
atom: Atom$n,
int: 
,
atom: Atom,
rec: rec(x.A[x]),
quotient: x,y:A//B[x; y],
tunion: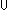 
x:A.B[x],
b-union: A 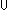B,
list: type List,
is_list_splitting: is_list_splitting(T;L;LL;L2;f),
is_accum_splitting: is_accum_splitting(T;A;L;LL;L2;f;g;x),
bag-member: bag-member(T;x;bs),
req: x = y,
rnonneg: rnonneg(r),
rleq: x 
y,
i-member: r 
I,
partitions: partitions(I;p),
modulus-of-ccontinuity: modulus-of-ccontinuity(omega;I;f),
fpf-sub: f 
g,
implies: P 
Q,
sq_stable: SqStable(P),
assert: 
b,
bool: 
,
true: True,
squash: 
T,
limited-type: LimitedType,
prop: 
,
it: 
,
inr: inr x ,
spread: spread def,
evalall: evalall(t),
rec-dataflow: rec-dataflow(s0;s,m.next[s; m]),
fpf: a:A fp-> B[a],
strong-subtype: strong-subtype(A;B),
le: A B,
ge: i 
j ,
not: 
A,
less_than: a < b,
uiff: uiff(P;Q),
subtype_rel: A r B,
set: {x:A| B[x]} ,
all: x:A. B[x],
axiom: Ax,
parallel-df-prog2: parallel-df-prog2(B;G;dfp1;dfp2),
so_apply: x[s1;s2],
nil: [],
df-program-meaning: df-program-meaning(dfp),
cons: [car / cdr],
select: l[i],
lambda: x.A[x],
natural_number: $n,
better-parallel-dataflow: better-parallel-dataflow,
function: x:A B[x],
df-program-type: df-program-type(dfp),
dataflow-program: DataflowProgram(A),
universe: Type,
uall: [x:A]. B[x],
so_lambda: 
x.t[x],
uimplies: b supposing a,
isect: 
x:A. B[x],
dataflow: dataflow(A;B),
and: P Q,
valueall-type: valueall-type(T),
equal: s = t,
Auto: Error :Auto,
CollapseTHEN: Error :CollapseTHEN,
inl: inl x ,
empty-bag: {},
pair: <a, b>,
apply: f a,
decide: case b of inl(x) => s[x] | inr(y) => t[y],
so_lambda: x y.t[x; y],
unit: Unit,
union: left + right,
bag: bag(T),
parameter: parm{i},
CollapseTHENA: Error :CollapseTHENA,
MaAuto: Error :MaAuto,
product: x:A 
B[x],
member: t T,
AssertBY: Error :AssertBY,
tactic: Error :tactic,
RepUR: Error :RepUR,
D: Error :D,
RepeatFor: Error :RepeatFor,
IdLnk: IdLnk,
Id: Id,
rationals: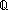 
,
so_apply: x[s],
or: P 
Q,
append: as @ bs,
guard: {T},
locl: locl(a),
Knd: Knd,
l_member: (x l),
void: Void,
subtype: S T,
top: Top,
pi1: fst(t),
pi2: snd(t)
Lemmas :
equal-unit,
pi1_wf_top,
pi2_wf,
rec-dataflow-equal,
top_wf,
bag_wf,
dataflow-program_wf,
valueall-type_wf,
df-program-type_wf,
uall_wf,
dataflow_wf,
empty-bag_wf,
member_wf,
unit_wf,
true_wf,
squash_wf,
rec-dataflow_wf,
evalall-equal,
parallel-2-equiv,
it_wf,
sq_stable__valueall-type,
product-valueall-type,
union-valueall-type,
equal-valueall-type,
bag-valueall-type
\mforall{}[A:\mBbbU{}']. \mforall{}[dfp1,dfp2:DataflowProgram(A)]. \mforall{}[B:Type]. \mforall{}[G:bag(df-program-type(dfp1))
{}\mrightarrow{} bag(df-program-type(dfp2))
{}\mrightarrow{} bag(B)].
better-parallel-dataflow(
2;\mlambda{}k.[df-program-meaning(dfp1); df-program-meaning(dfp2)][k];
\mlambda{}g.G[g 0;g 1])
= df-program-meaning(parallel-df-prog2(B;G;dfp1;dfp2))
supposing (G[\{\};\{\}] = \{\}) \mwedge{} valueall-type(B)
Date html generated:
2011_08_16-AM-09_42_47
Last ObjectModification:
2011_06_18-AM-08_33_27
Home
Index