{ 
[fun,arg:st_exp{i:l}()]. (ste_ap(fun;arg) 
st_exp{i:l}()) }
{ Proof }
Definitions occuring in Statement :
ste_ap: ste_ap(fun;arg),
st_exp: st_exp{i:l}(),
uall: [x:A]. B[x],
member: t T
Definitions :
tag-by: z
T,
ldag: LabeledDAG(T),
labeled-graph: LabeledGraph(T),
record+: record+,
record: record(x.T[x]),
fset: FSet{T},
dataflow: dataflow(A;B),
isect2: T1 
T2,
b-union: A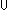 
B,
rev_implies: P 
Q,
or: P 
Q,
implies: P 
Q,
iff: P Q,
bag: bag(T),
list: type List,
set: {x:A| B[x]} ,
top: Top,
true: True,
prop: 
,
so_lambda: 
x.t[x],
type-monotone: Monotone(T.F[T]),
universe: Type,
eclass: EClass(A[eo; e]),
fpf: a:A fp-> B[a],
strong-subtype: strong-subtype(A;B),
le: A 
B,
ge: i 
j ,
not: 
A,
less_than: a < b,
uimplies: b supposing a,
and: P 
Q,
uiff: uiff(P;Q),
subtype_rel: A 
r B,
decision: Decision,
function: x:A 
B[x],
all: x:A. B[x],
axiom: Ax,
st_exp: st_exp{i:l}(),
ste_ap: ste_ap(fun;arg),
uall: [x:A]. B[x],
isect: x:A. B[x],
member: t T,
equal: s = t,
rec: rec(x.A[x]),
st-constant: st-constant{i:l}(Info),
union: left + right,
atom: Atom,
product: x:A B[x],
simple_type: Error :simple_type,
pair: <a, b>,
inr: inr x ,
inl: inl x
Lemmas :
Error :simple_type_wf,
st-constant_wf,
subtype_rel_wf,
uall_wf,
type-monotone_wf,
member_wf,
subtype_rel_sum,
subtype_rel_simple_product
\mforall{}[fun,arg:st\_exp\{i:l\}()]. (ste\_ap(fun;arg) \mmember{} st\_exp\{i:l\}())
Date html generated:
2011_08_17-PM-05_02_35
Last ObjectModification:
2011_02_04-AM-11_55_49
Home
Index