Step
*
2
1
of Lemma
sqrt-int-aa2
1. n : 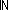 @i
@i
2. 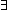 r:
r: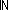 . (((r * r)
. (((r * r)  n)
n) 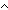 (n < ((r + 1) * (r + 1))))@i
(n < ((r + 1) * (r + 1))))@i

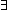 r:
r: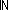 . (((r * r)
. (((r * r)  (n + 1))
(n + 1)) 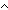 ((n + 1) < ((r + 1) * (r + 1))))
((n + 1) < ((r + 1) * (r + 1))))
BY
{ ((D (-1) THEN (Assert Dec((n + 1) < ((r + 1) * (r + 1))) BY MaAuto)) THEN D (-1)) }
1
1. n : 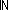 @i
@i
2. r : 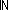 @i
@i
3. ((r * r)  n)
n) 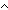 (n < ((r + 1) * (r + 1)))@i
(n < ((r + 1) * (r + 1)))@i
4. (n + 1) < ((r + 1) * (r + 1))

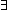 r:
r: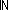 . (((r * r)
. (((r * r)  (n + 1))
(n + 1)) 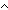 ((n + 1) < ((r + 1) * (r + 1))))
((n + 1) < ((r + 1) * (r + 1))))
2
1. n : 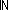 @i
@i
2. r : 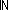 @i
@i
3. ((r * r)  n)
n) 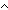 (n < ((r + 1) * (r + 1)))@i
(n < ((r + 1) * (r + 1)))@i
4. 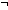 ((n + 1) < ((r + 1) * (r + 1)))
((n + 1) < ((r + 1) * (r + 1)))

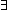 r:
r: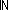 . (((r * r)
. (((r * r)  (n + 1))
(n + 1)) 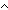 ((n + 1) < ((r + 1) * (r + 1))))
((n + 1) < ((r + 1) * (r + 1))))
1. n : \mBbbN{}@i
2. \mexists{}r:\mBbbN{}. (((r * r) \mleq{} n) \mwedge{} (n < ((r + 1) * (r + 1))))@i
\mvdash{} \mexists{}r:\mBbbN{}. (((r * r) \mleq{} (n + 1)) \mwedge{} ((n + 1) < ((r + 1) * (r + 1))))
By
((D (-1) THEN (Assert Dec((n + 1) < ((r + 1) * (r + 1))) BY MaAuto)) THEN D (-1))
Home
Index