The Book
Implementing Mathematics with The Nuprl Proof Development System
-
- Aczel 77
-
Peter Aczel.
An introduction to inductive definitions.
In Handbook of Mathematical Logic, J. Barwise, ed.
North-Holland, Amsterdam, 1977, pages 739-782.
- Aczel 78
-
Peter Aczel.
The type theoretic interpretation of constructive set theory.
In Logic Colloquium '77,
A. MacIntyre, L. Pacholaki, and J. Paris, eds.
North-Holland, Amsterdam, 1978, pages 55-66.
- Aho & Ullman 74
-
Alfred V. Aho and J. D. Ullman.
The Design and Analysis of
Computer Algorithms.
Addison-Wesley, Reading, MA, 1974.
- Aiello, Aiello, & Weyhrauch 77
-
L. Aiello, M. Aiello, and R. W. Weyhrauch.
Pascal in LCF: semantics and examples of proof.
Theoretical Computer Science, v. 5, n. 2 (1977)
pages 135-178.
- Allen 86
-
Stuart F. Allen.
The Semantics of Type Theoretic Languages.
Doctoral Dissertation, Computer Science Department,
Cornell University, August 1986 (expected).
- Anderson & Johnstone 62
-
John M. Anderson and Henry W. Johnstone.
Natural Deduction.
Wadsworth, Belmont, CA, 1962.
- Andrews 65
-
P. B. Andrews.
Transfinite Type Theory with Transfinite Type Variables.
North-Holland, Amsterdam, 1965.
- Andrews 71
-
P. B. Andrews.
Resolution in type theory.
J. Symbolic Logic, v. 36 (1971), pages 414-432.
- Artin, Grothendieck, & Verdier 72
-
M. Artin, A. Grothendieck, and J. L. Verdier.
Théories des topos et cohomologie étale des schémas.
In Lecture Notes in Mathematics, vols. 269 and 270.
Springer-Verlag, New York, 1972 (first appeared in 1963).
- Backhouse 84
-
Roland Backhouse.
A Note on Subtypes in Martin-Löf's Theory of Types.
Computer Science Department, University of Essex, England,
CSM-70, November 1984.
- Backhouse 85
-
Roland Backhouse.
Algorithm Development in Martin-Löf's Type Theory.
Computer Science Department, University of Essex, England, 1985.
- deBakker 80
-
Jaco deBakker.
Mathematical Theory of Program Correctness.
Prentice-Hall, Englewood Cliffs, NJ, 1980.
- Barringer, Cheng, & Jones 84
-
H. Barringer, J. H. Cheng, and C. B. Jones.
A Logic Covering Undefinedness in Program Proofs.
Department of Computer Science,
University of Manchester, England, 1984.
- Barwise 75
-
Jon Barwise.
Admissible Sets and Structures.
Springer-Verlag, New York, 1975.
- Barwise & Perry 83
-
Jon Barwise and John Perry.
Situations and Attitudes.
MIT Press, Cambridge, MA, 1983.
- Bates 79
-
Joseph L. Bates.
A Logic for Correct Program Development.
Doctoral Dissertation, Computer Science Department
Cornell University, 1979.
- Bates & Constable 85
-
Joseph L. Bates and Robert L. Constable.
Proofs as programs.
ACM Trans. Prog. Lang. Sys., v. 7, n. 1 (1985),
pages 113-136.
- Bates & Constable 83
-
J. L. Bates and R. L. Constable.
The Nearly Ultimate PRL.
Computer Science Department Technical Report,
TR-83-551.
Cornell University, Ithaca, NY, 1983.
- Beeson 81
-
M. J. Beeson.
Formalizing constructive mathematics: why and how?
In Constructive Mathematics, F. Richman, ed.,
Lecture Notes in Mathematics.
Springer-Verlag, New York, 1981, pages 146-190.
- Beeson 83
-
M. J. Beeson.
Proving programs and programming proofs.
In International Congress on Logic, Methodology and Philosophy of Science,
Salzburg, Austria.
North-Holland, Amsterdam, 1983.
- Beeson 85
-
M. J. Beeson.
Foundations of Constructive Mathematics.
Springer-Verlag, New York, 1985.
- Beth 56
-
E. W. Beth.
Semantic construction of intuitionistic logic.
Meded. Akad.
Amsterdam, N.R. 19, n. 11, (1956),
pages 357-388.
- Bibel 80
-
Wolfgang Bibel.
Syntax-directed, semantics-supported program synthesis.
Artificial Intelligence v. 14 (1980),
pages 243-261.
- Bibel 82
-
Wolfgang Bibel.
Automated Theorem Proving.
Sohn & Vieweg
Wiesbaden, West Germany, 1982.
- Bishop 67
-
Errett Bishop.
Foundations of Constructive Analysis.
McGraw-Hill, New York, 1967.
- Bishop 70
-
Errett Bishop.
Mathematics as a numerical language.
In Intuitionism and Proof Theory,
J. Myhill, et al., eds.
North-Holland, Amsterdam, 1970, pages 53-71.
- Bishop & Bridges 85
-
Errett Bishop and Douglas Bridges.
Constructive Analysis.
Springer-Verlag, New York, 1985.
- Bishop & Cheng 72
-
Errett Bishop and H. Cheng.
Constructive Measure Theory.
Mem. Am. Math. Soc. 116, 1972.
- Bledsoe 77
-
W. Bledsoe.
Non-resolution theorem proving.
Artificial Intelligence v. 9 (1977), pages 1-36.
- Bledsoe, Boyer, & Henneman 71
-
W. Bledsoe, R. Boyer, and W. Henneman.
Computer proofs of limit theorems.
Artificial Intelligence v. 2 (1971), pages 55-77.
- Bourbaki 68
-
N. Bourbaki.
Elements of Mathematics, Vol. I: Theory of Sets.
Addison-Wesley, Reading, MA, 1968.
- Boyer & Moore 79
-
R. Boyer and J. S. Moore.
A Computational Logic.
Academic Press, New York, 1979.
- Boyer & Moore 81
-
R. S. Boyer and J. S. Moore.
Metafunctions: proving them correct and
using them efficiently as new proof procedures.
In The Correctness Problem in Computer Science,
R. S. Boyer and J. S. Moore, eds.
Academic Press, New York, 1981, pages 103-184.
- Bridges 79
-
D. S. Bridges.
Constructive Functional Analysis.
Pitman, London, 1979.
- Brouwer 23
-
L. E. J. Brouwer.
On the significance of the principle of excluded middle
in mathematics, especially in function theory.
J. fur die Reine und Angewandte Math, v. 154,
(1923), 1-7.
In [vanHeijenoort 67], pages 334-345.
- Brouwer 75
-
L. E. J. Brouwer.
Vol. 1, Collected Works
A. Heyting, ed.
North-Holland, Amsterdam, 1975.
- deBruijn 70
-
N. G. deBruijn.
The mathematical language AUTOMATH, its usage and some of its extensions.
In Symposium on Automatic Demonstration,
Lecture Notes in Mathematics, Vol. 125.
Springer-Verlag, New York, 1970, pages 29-61.
- deBruijn 80
-
N. G. deBruijn.
A survey of the project AUTOMATH.
In Essays in Combinatory Logic, Lambda Calculus, and Formalism,
J. P. Seldin and J. R. Hindley, eds.
Academic Press, New York, 1980, pages 589-606.
- Buchholz et al. 81
-
W. Buchholz, S. Feferman, W. Pohlers, and W. Sieg.
Iterated Inductive Definitions and Subsystems of Analysis.
In Recent Proof-Theoretical Studies,
Lecture Notes in Mathematics, Vol. 897,
Springer-Verlag, New York, 1981.
- Bundy 83
-
Alan Bundy.
The Computer Modelling of Mathematical Reasoning.
Academic Press, New York, 1983.
- Burstall 69
-
R. Burstall.
Proving properites of programs by structural induction.
Comp. J. v. 12, n. 1, (1969), pages 41-48.
- Burstall & Lampson 84
-
R. M. Burstall and B. Lampson.
A kernel language for abstract data types and modules.
In Semantics of Data Types,
Lecture Notes in Computer Science, Vol. 173.
Springer-Verlag, New York, 1984 pages 1-50.
- Burstall, MacQueen, & Sanella 80
-
R. M. Burstall, D. B. MacQueen, and D. T. Sanella.
HOPE: an experimental applicative language.
In Proceedings 1980 Lisp Conference,
Computer Science Department,
Stanford University, Stanford, CA, 1980, pages 136-143.
- Cardelli 83
-
L. Cardelli.
The functional abstract machine.
Polymorphism: The ML/LCF/Hope Newsletter I (1983).
- Cardelli 84
-
L. Cardelli.
A semantics of multiple inheritance.
In Semantics of Data Types,
Lecture Notes in Computer Science, vol 173
Springer-Verlag, New York, 1984, pages 51-67.
- Cartwright 82
-
R. Cartwright.
Toward a logical theory of program data.
In Logics of Programs,
Lecture Notes in Computer Science Vol. 131.
Springer-Verlag, New York,
1982, pages 37-51.
- Chan 74
-
Y.-K. Chan.
Notes on constructive probability theory.
Ann. Probability, v. 2 (1974), pages 51-75.
- Charniak & McDermott 85
-
Eugene Charniak and Drew McDermott.
Introduction to Artificial Intelligence.
Addison-Wesley, Reading, MA, 1985.
- Chisholm 85
-
Paul Chisholm.
Derivation of a Parsing Algorithm in Martin-Löf's Theory of Types.
Department of Computer Science, Heriot-Watt University, Edinburgh,
Scotland, 1985.
- Church 40
-
A. Church.
A formulation of the simple theory of types.
J. Symbol. Logic v. 5, (1940), pages 56-68.
- Church 51
-
Alonzo Church.
The calculi of lambda-conversion.
Annals of Mathematics Studies, No. 6.
Princeton University Press, Princeton, NJ, 1951.
- Clarke & Emerson & Sistla 83
-
Edmond M. Clarke, Jr., E. A. Emerson and A. P. Sistla.
Automatic verification of finite state concurrent systems
using temporal logic specification: a practical approach.
In 10th ACM Symposium on Principles of
Programming Languages.
ACM, New York, 1983.
- Cleaveland 86
-
W. Rance Cleaveland.
Type Theoretic Models of Concurency.
Doctoral Dissertation,
Computer Science Department,
Cornell University 1986.
- Clocksin & Mellish 81
-
W. F. Clocksin and C. S. Mellish.
Programming in Prolog.
Springer-Verlag, New York, 1981.
- Constable 71
-
Robert L. Constable.
Constructive mathematics and automatic programs writers.
In Proceedings of IFIP Congress, Ljubljana,
1971, pages 229-233.
- Constable 77
-
Robert L. Constable.
On the theory of programming logics.
In Proceedings of the 9th Annual ACM Symposium on Theory of Computing,
Boulder, Colorado, May 1977, pages 269-285.
- Constable 83
-
Robert L. Constable.
Programs as proofs.
Inform. Processing Lett., v. 16, n. 3, (1983),
pages 105-112.
- Constable 85
-
Robert L. Constable.
Constructive mathematics as a programming logic I: some principles of theory.
Ann. Discrete Math., v. 24 (1985),
pages 21-38.
- Constable & Mendler 85
-
Robert L. Constable and N. P. Mendler.
Recursive definitions in type theory.
In Proceedings of Logics of Programs Conference,
Lecture Notes in Computer Science,
Springer-Verlag, New York, 1985, pages 61-78.
- Constable, Johnson, & Eichenlaub 82
-
Robert L. Constable, Scott D. Johnson, and Carl D. Eichenlaub.
Introduction to the PL/CV2 Programming Logic,
Lecture Notes in Computer Science, Vol. 135,
Springer-Verlag, New York, 1982.
- Constable, Knoblock, & Bates 84
-
Robert L. Constable, Todd B. Knoblock, and Joseph L. Bates.
Writing programs that construct proofs.
J. Automated Reasoning, v. 1 n. 3,
(1984), pages 285-326.
- Constable & O'Donnell 78
-
Robert L. Constable and Michael J. O'Donnell.
A Programming Logic.
Winthrop, Cambridge, MA, 1978.
- Constable & Zlatin 84
-
Robert L. Constable and Daniel R. Zlatin.
The type theory of PL/CV3.
ACM Trans. Prog. Lang. Sys., v. 7, n. 1 (1984),
pages 72-93.
- Coquand & Huet 85
-
Thierry Coquand and Gerard Huet.
Constructions: A Higher Order Proof
System for Mechanizing Mathematics.
EUROCAL 85, Linz, Austria, April 1985.
- Curry, Feys, & Craig 58
-
H. B. Curry, R. Feys, and W. Craig.
Combinatory Logic, Vol. 1.
North-Holland, Amsterdam, 1958.
- Curry, Hindley, & Seldin 72
-
H. B. Curry, J. R. Hindley, and J. P. Seldin.
Combinatory Logic, Vol. 2.
North-Holland, Amsterdam, 1972.
- van Daalen 80
-
Diedrik T. van Daalen.
The Language Theory of AUTOMATH.
Doctoral Dissertation, Technical University of Eindhoven,
1980.
- Davis 65
-
M. Davis, ed.
The Undecidable.
Raven Press, New York, 1965.
- Davis & Lenat 82
-
Randall Davis and Douglas B. Lenat.
Knowledge-Based Systems in
Artificial Intelligence.
McGraw-Hill, New York, 1982.
- Davis & Schwartz 79
-
M. Davis and J. T. Schwartz.
Metamathematical extensibility for theorem
verifiers and proof checkers.
Comp. Math. with Applications, v. 5 (1979),
pages 217-230.
- Dijkstra 76
-
Edsger W. Dijkstra.
A Discipline of Programming.
Prentice-Hall, Englewood Cliffs, NJ, 1976.
- Donahue & Demers 79
-
J. E. Donahue and A. J. Demers.
Revised Report on Russell.
Computer Science Department
Technical Report, TR 79-389.
Cornell University, Ithaca, NY, September 1979.
- Donahue & Demers 85
-
J. E. Donahue and A. J. Demers.
Data types are values.
TOPLAS, v. 7, n. 3, (July 1985), pages 426-445.
- Donzeau-Gouge et al. 80
-
Veronique Donzeau-Gouge, Gerard Huet, Gilles Kahn, and Bernard Lang.
Programming environments based on structured editors:
the Mentor experience.
INRIA, Rapports de Recherches, No. 26, July 1980.
- Doyle 79
-
John Doyle.
A truth maintenance system.
Artificial Intelligence, v. 12, n. 3.
(1979), pages 231-272.
- Dummet 77
-
Michael Dummett.
Elements of Intuitionism, Oxford Logic Series.
Clarendon Press, Oxford, 1977.
- Feferman 79
-
S. Feferman.
Constructive theories of functions and classes.
In Logic Colloquium '78,
North-Holland, Amsterdam, 1979, pages 159-224.
- Fitch 52
-
Frederic B. Fitch.
Symbolic Logic.
Roland Press, New York 1952
- Fitting 83
-
M. Fitting.
Proof Methods for Modal and Intuitionistic Logics.
D. Reidel, Dordrecht, The Netherlands, 1983.
- Fortune, Leivant, & O'Donnell 83
-
S. Fortune, D. Leivant, and M. O'Donnell.
The expressiveness of simple and second order type structures.
J. ACM, v. 30 (1983),
pages 151-185.
- Frege 1879
-
Gottlob Frege.
Begriffsschrift, a formula language, modeled upon that for arithmetic,
for pure thought.
In [vanHeijenoort 67], pages 1-82.
- Friedman 73
-
Harvey Friedman.
The consistency of classical set theory
relative to set theory with intuitionistic logic.
J. Symbolic Logic, v. 56, n. 38 (1973),
pages 315-319.
- Gabby 81
-
Dov Gabby.
Semantical Investigations in Heyting's Intuitionistic Logic.
D. Reidel, Dordrecht, The Netherlands, 1981.
- Gentzen 69
-
Gerhard Gentzen.
Investigations into logical deduction.
In The Collected Papers of Gerhard Gentzen, M. E. Szabo, ed.
North-Holland, Amsterdam, 1969.
- Girard 71
-
J. Y. Girard.
Une extension de l'interpretation de Godel a l'analyse,
et son application a l'elimination des coupures dans l'analyse et la
theorie des types.
In 2nd Scandinavian Logic Symposium,
J. E. Fenstad, ed.
North-Holland, Amsterdam, 1971, pages 63-92.
- Goad 80
-
C. Goad.
Proofs as descriptions of computation.
In Proceedings of the 5th Conference
on Automated Deduction
Les Arcs, France,
Lecture Notes in Computer Science, Vol. 87,
Springer-Verlag, New York, 1980, pages 39-52.
- Goguen, Thatcher & Wagner 78
-
J. A. Goguen, J. W. Thatcher and E. G. Wagner.
Initial algebra approach to the specification,
correctness and implementation of abstract data types.
In Current Trends in Programming Methodology, Vol. IV, R.
Yeh, ed.
Prentice-Hall, Englewood Cliffs, NJ, 1978.
- Goldblatt 79
-
Robert Goldblatt.
TOPI: The Categorial Analysis of Logic.
North-Holland, Amsterdam, 1979.
- Goodman 84
-
Nicolas D. Goodman.
Epistemic arithmetic is a Conservative Extension
of Intuitionistic Arithmetic.
J. Symbolic Logic, v. 49, n. 1 (1984),
pages 192-204.
- Goodman & Myhill 72
-
Nicolas D. Goodman and John Myhill.
The formalization of Bishop's constructive
mathematics.
Toposes, Algebraic Geometry and Logic,
Lecture Notes in Mathematics, Vol. 274.
Springer-Verlag, New York, 1972, pages 83-96.
- Gordon, Milner, & Wadsworth 79
-
Michael Gordon, Arthur Milner, and Christopher Wadsworth.
Edinburgh LCF: A Mechanized Logic of Computation,
Lecture Notes in Computer Science, Vol. 78
Springer-Verlag, New York, 1979.
- Goto 79
-
S. Goto.
Program synthesis from natural deduction proofs.
International Joint Conference on Artificial Intelligence,
Tokyo, 1979.
- Gries 78
-
David Gries, ed.
Programming Methodology: A Collection of Articles by Members of IFIP WG2.3.
Springer-Verlag, New York, 1978.
- Gries 81
-
David Gries.
The Science of Programming.
Springer-Verlag, New York, 1981.
- Guttag & Horning 78
-
J. Guttag and J. Horning.
The algebraic specification of abstract data types.
In Programming Methodology, D. Gries, ed.
Springer-Verlag, New York. 1978.
- Harper 85
-
Robert W. Harper.
Aspects of the Implementation of Type Theory.
Doctoral Dissertation,Computer Science Department,
Cornell University, June 1985.
- Hehner 79
-
E. C. R. Hehner.
do considered od: a contribution to the programming calculus.
Acta Informatica, v. 11, n. 4 (1979),
pages 287-304.
- vanHeijenoort 67
-
J. van Heijenoort.
From Frege to Gödel: A Sourcebook in Mathematical Logic.
Harvard University Press, Cambridge, MA, 1967.
- Heyting 30
-
Arend Heyting.
Die formalen Regeln der intuitionistischen Logik.
Sitzungsber. Preuss. Akad. Wiss.,
Phys. - Math Kl.,
1930, pages 42-56.
- Heyting 56
-
Arend Heyting.
Intuitionism: An Introduction.
North-Holland, Amsterdam, 1956.
- Hoare 72
-
C. A. R. Hoare.
Notes on data structuring.
In Structured Programming.
Academic Press, New York, 1972, pages 83-174.
- Howard 80
-
W. Howard.
The formulas-as-types notion of construction.
In To H. B. Curry: Essays on Combinatory Logic, Lambda-Calculus,
and Formalism, J. P. Seldin and J. R. Hindley, eds.
Academic Press, New York, 1980, pages 479-490.
- Howe 86
-
Douglas J. Howe.
Implementing Analysis.
Doctoral Dissertation,
Computer Science Department,
Cornell University, 1986 (expected).
- Huet 75
-
Gerard P. Huet.
A unification algorithm for typed lambda-calculus.
Theoretical Computer Science, v. 1, n. 1 (1975),
pages 27-58.
- Johnson 83
-
Scott D. Johnson.
A Computer System for Checking Proofs.
UMI Press, New York, 1983.
- Jutting 79
-
L. S. Jutting.
Checking Landau's ``Grundlagen'' in the AUTOMATH System.
Doctoral Thesis,
Eindhoven University, Eindhoven, The Netherlands, 1977.
Also in Math. Centre Tracts No. 83, Math. Centre, Amsterdam, 1979.
- Kay 77
-
Alan Kay.
Microelectronics and the Personal Computer.
Scientific American, September, 1977.
- Kay & Goldberg 77
-
Alan Kay and Adele Goldberg.
Personal dynamic media.
Computer, v. 31, (March 1977).
- Kleene 45
-
Stephen C. Kleene.
On the interpretation of intuitionistic number theory.
J. Symbolic Logic v. 10 (1945),
pages 109-124.
- Kleene 52
-
Stephen C. Kleene.
Introduction to Metamathematics.
Van Nostrand, Princeton, NJ, 1952.
- Kleene & Vesley 65
-
Stephen C. Kleene and R. E. Vesley.
The Foundations of Intuitionistic Mathematics.
North-Holland, Amsterdam, 1965.
- Knoblock 86
-
Todd B. Knoblock.
Formal Metamathematics and Reflection in
Constructive Type Theory.
Doctoral Dissertation,
Computer Science Department, Cornell University, 1986.
- Knuth 68
-
D. E. Knuth.
The Art of Computer Programming, Vol. I.
Addison-Wesley, Reading, MA, 1968.
- Kowalski 79
-
Robert Kowalski.
Logic for Problem Solving.
North-Holland, New York, 1979.
- Kozen 77
-
Dexter C. Kozen.
Complexity of Finitely Presented Algebras.
Doctoral Dissertation, Computer Science Department,
Cornell University, 1977.
- Krafft 81
-
Dean B. Krafft.
AVID: A System for the Interactive Development of Verifiably Correct
Programs.
Doctoral Dissertation, Computer Science Department
Cornell University, 1981.
- Kreisel 62
-
G. Kreisel.
Foundations of intuitionistic logic.
In Logic, Methodology
and Philosophy of Science
Stanford University Press, Stanford, CA,
1962, pages 198-210.
- Kreisel 70
-
G. Kreisel.
Hilbert's program and the search for automatic proof procedures.
In Symposium on Automatic Demonstration, Lecture Notes in Mathematics, Vol. 125.
Springer-Verlag, New York (1970), pages 128-146.
- Lakatos 76
-
Imre Lakatos.
Proofs and Refutations.
Cambridge University Press, Cambridge, 1976.
- Lambek 80
-
J. Lambek.
From types to sets.
Advances in Mathematics v. 35 (1980).
- Lauchli 70
-
H. Lauchli.
An abstract notion of realizability for which
intuitionistic predicate calculus is complete.
In Intuitionism and Proof Theory, J. Myhill, A. Kino,
and R. E. Vesley, eds.
North-Holland, Amsterdam, 1970, pages 227-234.
- Leivant 83
-
Daniel Leivant.
Structural semantics for polymorphic data types
(preliminary report).
In Proceedings of the 10th ACM Symposium in the Principles of Programming Languages, ACM, New York,
1983, pages 155-166.
- Linger, Mills & Witt 79
-
R. C. Linger, H. D. Mills and B. I. Witt.
Structured Programming Theory and Practice.
Addison-Wesley, Reading, MA, 1979.
- Loveland 78
-
Donald W. Loveland.
Automated Theorem Proving: A Logical Basis.
North-Holland, Amsterdam, 1978.
- MacLane 69
-
Saunders MacLane.
Foundations for categories and sets.
In Category Theory, Homology Theory and Their Applications II,
Lecture Notes in Mathematics, Vol. 92.
Springer-Verlag, New York, 1969,
pages 146-164.
- MacQueen 85
-
David B. MacQueen.
Modules for Standard ML.
Polymorphism Newsletter, v. 2, n. 2 (1985).
- MacQueen, Plotkin, & Sethi 84
-
D. B. MacQueen, G. D. Plotkin, and R. Sethi.
An ideal model for recursive polymorphic types.
In 11th ACM Symposium on Principles of Programming Languages,
1984, pages 165-174.
- Manna & Waldinger 80
-
Z. Manna and R. Waldinger.
A deductive approach to program synthesis.
ACM Trans. Prog. Lang. Sys. v. 2 n. 1 (1980),
pages 90-121.
- Manna & Waldinger 85
-
Z. Manna and R. Waldinger.
The Logical Basis for Computer Programming.
Addison-Wesley, Reading, MA, 1985.
- Martin-Löf 70
-
Per Martin-Löf.
Notes on Constructive Mathematics.
Almqvist & Wiksell, Stockholm, 1970.
- Martin-Löf 71
-
Per Martin-Löf.
Hauptsatz for the intuitionistic theory of
iterated inductive definitions,
In Proceedings of the Second Scandinavian
Logic Symposium, J. E. Fenstad ed.
North-Holland, Amsterdam, 1971, pages 179-216.
- Martin-Löf 73
-
Per Martin-Löf.
An intuitionistic theory of types: predicative part.
In Logic Colloquium '73,
H. E. Rose and J. C. Shepherdson, eds.
North-Holland, Amsterdam, 1973, pages 73-118.
- Martin-Löf 82
-
Per Martin-Löf.
Constructive mathematics and computer programming.
In Sixth International Congress for Logic, Methodology,
and Philosophy of Science.
North-Holland, Amsterdam, 1982, pages 153-175.
- Martin-Löf 84
-
Per Martin-Löf.
Intuitionistic Type Theory.
Studies in Proof Theory Lecture Notes, BIBLIOPOLIS, Napoli, 1984.
- The Mathlab Group 77
-
The Mathlab Group.
MACSYMA Reference Manual.
MIT, December 1977.
- McAllester 82
-
David A. McAllester.
Reasoning Utility Package User's Manual, Version One.
AI Lab. MIT, AIM-667, April 1982.
- McCarthy 62
-
J. McCarthy.
Computer programs for checking mathematical proofs.
In Proceedings of the Symposia in Pure Mathematics, Vol. V, Recursive
Function Theory.
American Mathematical Society, Providence, RI, 1962.
- McCarthy 63
-
J. McCarthy.
A basis for a mathematical theory of computation.
In Computer Programming and Formal Systems.
P. Braffort and D. Herschberg, eds.
North-Holland, Amsterdam, 1963, pages 33-70.
- McCarty 84
-
David C. McCarty.
Realizability and recursive mathematics.
Doctoral Dissertation,
Computer Science Department,
Carnegie-Mellon University, 1984.
- McGettrick 78
-
A. D. McGettrick.
Algol 68, A First and Second Course.
Cambridge University Press, Cambridge, 1978.
- Mendler 86
-
N. P. Mendler.
Recursive Types and Infinite Objects.
Doctoral Dissertation, Computer Science Department
Cornell University, 1986 (expected).
- Metakides & Nerode 79
-
G. Metakides and A. Nerode.
Effective content of field theory.
Ann. Math. Logic, v. 17 (1979),
pages 289-320.
- Meyer 82
-
Albert R. Meyer.
What is a model of the lambda calculus?
Information and Control, v. 52, n. 1 (1982),
pages 87-122.
- Milner 85
-
R, Milner.
The standard ML core language.
Polymorphism Newletter, v. 2, n. 2 (1985),
pages 1-28.
- Milner & Weyhrauch 72
-
R. Milner and R. Weyhrauch.
Proving computer correctness in mechanized logic.
In Machine Intelligence Vol. 7,
B. Meltzer and D. Michie, eds.),
Edinburgh University Press,
Edinburgh, Scotland, 1972, pages 51-70.
- Minsky 81
-
Marvin Minsky.
A framework for representing knowledge.
In Mind Design, J. Haugeland, ed.
MIT Press, Cambridge, MA, 1981, pages 95-128.
- Mitchell & Plotkin 85
-
John Mitchell and Gordon Plotkin.
Abstract types have existential type.
In Proceedings of 12th ACM Symposium on
Principles of Programming Languages.
ACM, New York, 1985, pages 37-51.
- Morse 65
-
A. Morse.
A Theory of Sets.
Academic Press, New York, 1965.
- Moschovakis 74
-
Yiannis N. Moschovakis.
Elementary Induction on Abstract Structures.
North-Holland, Amsterdam, 1974.
- Mulmuley 84
-
K. Mulmuley.
Mechanization of existence proofs of recursive functions.
In Proceedings 7th International Conference
on Automated Deduction.
Lecture Notes in Computer Science, Vol. 170.
Springer-Verlag, New York, 1984, pages 460-475.
- Myhill 75
-
J. Myhill.
Constructive Set Theory.
J. Symbol. Logic, v. 40 (1975),
pages 347-383.
- Nederpelt 80
-
R. P. Nederpelt.
A system of natural reasoning based on a typed
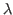 -calculus.
-calculus.
Bull. Eur. Assoc. Theoret. Comp. Sci., v. 11 (1980),
pages 130-131.
- Nelson & Oppen 79
-
Greg Nelson and Derek C. Oppen.
Simplification by cooperating decision procedures.
ACM Trans. Prog. Lang. Sys. v. 1, n. 2 (1979),
pages 245-257.
- Nepeivoda 82
-
N. N. Nepeivoda.
Logical approach to programming.
In Sixth International Congress for
Logic, Methodology and Philosophy of Science
North-Holland, Amsterdam, 1982, pages 109-122.
- Nordstrom 81
-
Bengt Nordstrom.
Programming in constructive set theory: some examples.
In Proceedings 1981 Conference on Functional
Programming Languages
and Computer Architecture.
Portsmouth, England, 1981, pages 141-153.
- Nordstrom & Petersson 83
-
Bengt Nordstrom and Kent Petersson.
Types and specifications.
In Proceedings IFIP '83, R. E. A. Mason, ed.
North-Holland, Amsterdam, 1983, pages 915-920.
- Nordstrom & Smith 84
-
Bengt Nordstrom and Jan Smith.
Propositions, types, and specifications in Martin-Löf's type theory.
BIT, v. 24, n. 3 (1984), pages 288-301.
- Nuprl Staff 83
-
The Nuprl Staff.
PRL: Proof Refinement Logic Programmer's Manual (Lambda PRL, VAX Version).
Computer Science Department, Cornell University, New York, 1983.
- O'Donnell 85
-
Michael J. O'Donnell.
Equational Logic as a Programming Language.
MIT Press, Cambridge, MA, 1985.
- Paterson & Wegman 78
-
M. S. Paterson and M. N. Wegman.
Linear unification, J. CSS, v. 16 (1978),
pages 158-197.
- Paulson 83a
-
Lawrence Paulson.
Tactics and Tacticals in Cambridge LCF.
Technical Report 39,
Computer Laboratory,
University of Cambridge, July 1983.
- Paulson 83b
-
Lawrence Paulson.
A higher-order implementation of rewriting.
Sci. Comp. Programming, n. 3 (1983),
pages 119-149.
- Paulson 84
-
Lawrence Paulson.
Verifying the Unification Algorithm in LCF.
Technical Report 50,
Computer Laboratory,
University of Cambridge, March 1984.
- Paulson 85
-
Lawrence Paulson.
Lessons learned from LCF: a survey of natural deduction proofs.
Comp. J. v. 28 n. 5 (1985).
- Petersson 82
-
Kent Pertersson
A Programming System for Type Theory.
Memo 21, Programming Methodology Group,
University of Götberg/Chalmers,
Götberg, Sweden, March 1982.
- Petersson & Smith 85
-
Kent Petersson and Jan Smith.
Program Derivation in Type Theory: The Polish Flag Problem.
Computer Science Department, University of Götberg/Chalmers,
Götberg, Sweden, January 1985.
- Platek 66
-
Richard Alan Platek.
Foundations of Recursion Theory.
Doctoral Dissertation, Stanford University, 1966.
- Plotkin 77
-
Gordon D. Plotkin.
LCF considered as a programming language.
Theoretical Computer Science, v. 5 (1977),
pages 223-257.
- Poincaré 82
-
Henri Poincaré.
The Foundations of Science.
University Press of
America, Washington, DC, 1982.
- Post 43
-
E. Post.
Formal reductions of the general combinatorial decision problem.
American J. Math, v. 65 (1943)
pages 197-215.
- Prawitz 70
-
D. Prawitz.
Ideas and results in proof theory.
In Proceedings of the Second Scandinavian
Logic Symposium,
J. E. Fenstad, ed.
North-Holland, Amsterdam, 1970, pages 235-308.
- Quine 63
-
Willard Van Orman Quine.
Set Theory and Its Logic.
Belknap Press,
Combridge, MA, 1963.
- Reps 84
-
Thomas W. Reps.
Generating Language-Based Environments.
MIT Press, Cambridge, MA, 1984.
- Reps & Alpern 84
-
Thomas W. Reps and B. Alpern.
Interactive proof checking.
In 11th ACM Symposium on
Principles of Programming Languages.
ACM, New York, 1984.
- Reps & Teitelbaum 85
-
Thomas W. Reps and Tim Teitelbaum.
The Synthesizer Generator Reference Manual,
Computer Science Department,
Technical Report, TR 84-619,
Cornell University, Ithaca, NY,
August 1985.
- Reynolds 74
-
John C. Reynolds.
Towards a theory of type structure.
In Proceedings Colloque sur la Programmation,
Lecture Notes in Computer Science Vol. 19.
Springer-Verlag, New York, 1974, pages 408-423.
- Reynolds 83
-
John C. Reynolds.
Types, abstraction, and parametric polymorphism.
In Information Processing 83.
North-Holland, Amsterdam, 1983, pages 513-523.
- Richman 81
-
F. Richman, ed.
Constructive Mathematics.
Lecture Notes in Mathematics, Vol. 873,
Springer-Verlag, New York, 1981.
- Robinson 65
-
J. A. Robinson.
A machine-oriented logic based on the resolution principle.
J. ACM v. 12 (1965),
pages 23-41.
- Robinson 71
-
J. A. Robinson.
Computational logic: the unification algorithm.
In Machine Intelligence Vol. 6,
B. Meltzer and D. Michie, eds.
Edinburgh University Press,
Edinburgh, Scotland, 1971, pages 63-72.
- Russell 08
-
Bertrand Russell.
Mathematical logic as based on a theory of types.
Am. J. of Math., v. 30 (1908),
pages 222-262.
- Russell 56
-
Bertrand Russell.
In Logic and Knowledge, R. D. Marsh, ed.
George Allen & Unwin, London, 1956.
- Sasaki 85
-
James T. Sasaki.
The Extraction and Optimization of Programs from Constructive Proofs.
Doctoral Dissertation, Computer Science Department,
Cornell University, 1985.
- Scherlis & Scott 83
-
W. L. Scherlis and D. Scott.
First steps toward inferential programming.
In Proceedings IFIP Congress, Paris, 1983.
- Schutte 77
-
Kurt Schutte.
Proof Theory.
Springer-Verlag, New York, 1977.
- Scott 70
-
Dana Scott.
Constructive validity.
In Symposium on Automatic Demonstration,
Lecture Notes in Mathematics, Vol. 125.
Springer-Verlag, New York, 1970, pages 237-275.
- Scott 76
-
Dana Scott.
Data types as lattices.
SIAM J. Computing, v. 5 (1976), pages 522-587.
- Shankar 84
-
N. Shankar.
Towards Mechanical Metamathematics.
Institute for Computing Science
Technical Report 43,
University of Texas at Austin, 1984.
- Shultis 85
-
Jon Shultis.
INTUIT: A System for Program Synthesis Using
Intuitionistic Logic (draft).
Computer Science Department
University of Colorado, July 1985.
- Siekmann & Wrightson 83
-
Jorg Siekmann and Graham Wrightson.
Automation of Reasoning,
Classical Papers on Computational Logic:
Vol. 1, 1957-1966;
Vol. 2, 1967-1970.
Springer-Verlag, New York, 1983.
- Smith 84
-
Jan Smith.
An interpretation of Martin-Löf's type theory in a type-free theory
of propositions.
J. Symbol. Logic, v. 49, n. 3 (1984),
pages 730-753.
- Smullyan 68
-
Raymond M. Smullyan.
First-Order Logic.
Springer-Verlag, New York, 1968.
- Sokolowski 83
-
S. Sokolowski.
A Note on Tactics in LCF.
Department of Computer Science,
Report CSR-140-83,
University of Edinburgh, Edinburgh, Scotland, 1983.
- Stansifer 85
-
Ryan D. Stansifer.
Representing Constructive Theories in
High-Level Programming Languages.
Doctoral Dissertation, Computer Science Department,
Cornell University, 1985.
- Statman 79
-
R. Statman.
Intuitionistic Propositional Logic
is Polynomial-space Complete,
Theoretical Computer Science, v. 9, (1979), pages 73-81.
- Steele 84
-
Guy L. Steele.
Common LISP - The Language.
Digital Press, Burlington, MA, 1984.
- Stenlund 72
-
Sören Stenlund.
Combinators, 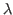 -terms, and Proof Theory.
-terms, and Proof Theory.
D. Reidel, Dordrecht, The Netherlands, 1972.
- Stoy 77
-
Joseph E. Stoy.
Denotational Semantics: The Scott-Strachey
Approach to Programming Language Theory.
MIT Press, Cambridge, MA, 1977.
- Suppes 81
-
P. Suppes.
University-Level Computer-Assisted Instruction at Stanford: 1968-1981.
Institute for Mathematical Studies in the Social
Sciences, Stanford University, Stanford, CA, 1981.
- Tait 67
-
William W. Tait.
Intensional interpretation of functionals of finite type.
J. Symbol. Logic, v. 32, n. 2 (1967),
pages 187-199.
- Takasu 78
-
A. S. Takasu.
Proofs and programs,
In Proceedings of the Third IBM Symposium
on the Mathematical
Foundations of Computer Science,
Kansai, 1978.
- Takeuti 75
-
Gaisi Takeuti.
Proof Theory.
North-Holland, Amsterdam, 1975.
- Teitelbaum & Reps 81
-
R. Teitelbaum and T. Reps.
The Cornell program synthesizer:
a syntax-directed programming environment.
Commun. ACM, v. 24, n. 9 (1981),
pages 563-573.
- Toledo 75
-
Sue Ann Toledo.
Tableau systems for first order number
theory and certain higher order theories.
In Lecture Notes in Mathematics Vol. 447
Springer-Verlag, New York, 1975.
- Troelstra 73
-
Ann S. Troelstra.
Metamathematical Investigation of Intuitionistic Arithmetic and Analysis,
Lecture Notes in Mathematics, Vol. 344.
Springer-Verlag, New York, 1973.
- Troelstra 77
-
Ann S. Troelstra.
Choice Sequences: A Chapter of Intuitionistic Mathematics.
Claredon Press, Oxford, 1977.
- Turner 84
-
Raymond Turner.
Logics for Artificial Intelligence.
Halsted Press
(John Wiley & Sons), New York, 1984.
- Weyhrauch 80
-
R. Weyhrauch.
Prolegomena to a theory of formal reasoning.
Artificial Intelligence, v. 13, (1980),
pages 133-170.
- Whitehead & Russell 25
-
A. N. Whitehead and B. Russell.
Principia Mathematica, Vol. 1.
Cambridge University Press, Cambridge, MA, 1925.
- Wos et al. 84
-
Larry Wos, R. Overbeek, L. Ewing, and J. Boyle.
Automated Reasoning.
Prentice-Hall, Englewood Cliffs, NJ, 1984.
- Zucker 75
-
J. Zucker.
Formalization of classical mathematics in AUTOMATH.
In Colloques Internationaux du Centre Nationale
de la Recherche Scientifique, No. 249,
1975, pages 136-145.

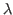 -calculus.
-calculus.
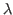 -terms, and Proof Theory.
-terms, and Proof Theory.

