EventML Software

A functional programmming language with high level combinators that works with the Nuprl theorem prover

EventML Documentation

Introduction to EventML 0.2 [PDF]
Introduction to Event ML 0.2 [HTML] 3/2012

Introduction to Classic ML for EventML [PDF]

Download

EventML is available as
Linux version
nuprl-web.cs.cornell.edu/software/eventml/eventml_0.3-src.tar.gz (rev. 9/21/2012)
See Archive at left for earlier versions and Windows version.
note: see the README file for help

EventML

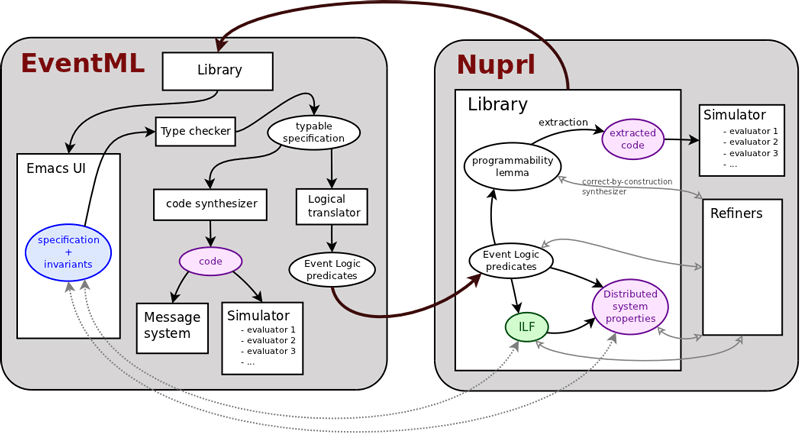
is a functional programming language in the ML family, closely related to Classic ML. It is also a language for coding distributed protocols (such as Paxos) using high level combinators from the Logic of Events (or Event Logic), hence the name “EventML”.

The Event Logic combinators are high level specifications of distributed computations whose properties can be naturally expressed in Event Logic. The combinators can be formally translated (compiled) into the process model underlying Event Logic and thus converted to distributed programs. The interactions of these high level distributed programs manifest the behavior described by the logic. EventML can thus both specify and execute the processes that create the behaviors, called event structures, arising from the interactions of the processes.

EventML

EventML was created to work in cooperation with an interactive theorem prover and to be a key component of a Logical Programming Environment (LPE).

In one direction, EventML can import logical specifications from the prover as well as event class specifications and the process code that realizes them. In the present mode of operation, EventML docks with the Nuprl prover to obtain this information.

In the other direction, EventML can be used by programmers to specify protocols using event logic combinators.

Read more in the Introduction to EventML [PDF]

About EventML-
A Logical Programming Environment (LPE)

EventML is an interface to components of a Logical Programming Environment (LPE) developed by the PRL group [1]. The four main components of this LPE are:

1. its library which is a large database where definitions (also called abstractions), theorem statements and proofs are stored, in particular those of the Logic of Events (see below)
2. the Nuprl interactive theorem prover which communicates with the library to perform refinement steps and build proofs
3. evaluators for computable terms
4. its structured editor.

A Logic of Events

The Logic of Events [2, 3] is a logic developed to deal with: (1) events; (2) their spacial locations (or just locations for short); and (3) their temporal locations obtained via a well-founded relation ordering these events (a temporal ordering). The Logic of Events also provides ways to describe the nature of events and their associated information. We will only consider the case where each event is triggered by a message which is called its primitive information. For example, some distributed algorithms start performing actions upon reception of certain kind of messages. The events corresponding to these messages can be considered as input events to such systems. An event ordering is a structure composed by: (1) a set of events, (2) a location function that associate a location with each event, (3) an information function that associates a primitive information with each event, and (4) an ordering relation on events. Important events are exchanges of messages: the Logic of Events is based on a model of message passing.

An important concept in the Logic of Events is the one of event classes [2]. Concurrent systems can be specified by classifying the different events that can occur. An event class is a function that partitions the events of an event ordering into two sets by associating values to only some of the events. In an event ordering eo, an event e is in a class X if X associates a value with e. An event class can sometimes be regarded as a process that, given an event in the class, produces some value (e.g., a message along with the recipient's location) from the message that triggered the event.

What is EventML?

EventML can be regarded as an interface to the Logic of Events to primarily ease the specification of concurrent systems' behavior. It was originally defined as a language for defining components of distributed systems [2]. More specifically, EventML's language is a core language based on classic ML and on the Logic of Events. It allows specifying information flow of concurrent systems at a high level of abstraction. Such a specification is itself an EventML program.

EventML's language is higher-order and strongly typed, with almost full type inference. Full type inference is useful to, e.g., free programmers from the burden of having to write down types. We say "almost" because in EventML types are sometimes required (i.e., programmers have to sometimes provide type information to help the type inference procedure), e.g., to specify, for each message header header involved in a specification, the type of the values sent in messages with header header. EventML's type inference algorithm is based on ML's.

The EventML tool consists of the following modules: a parser, a type checker, a sanitizer, and an interpreter. Let us briefly discuss these different parts.

EventML's type inferencer is constraint-based [6, 7, 8], i.e., it is composed by two phases: (1) first, given a piece of code, constraints (e.g., type equality constraints) are generated; (2) then, a constraint solver is used to solve the generated constraints and therefore check the typablity of the piece of code. Constraint-based type inferencer, among other things, allow one to do type error slicing [4, 5, 9] (see below). Once an EventML program type checks, our EventML tool runs a sanitizer on the program. This sanitizer checks, among other things, that for each use of the binary equality operator "=", a Nuprl equality decider can be generated. For example, let f x1 x2 = (x1 = x2);; type checks but EventML cannot generate an equality decider for the polymorphic use of "=". To solve such problems, one can, e.g., restrict the types of the arguments using type constraints as follows: let f (x1 : Int) x2 = (x1 = x2);;. When interpreting this piece of code, the EventML tool automatically applies the integer equality decider to x1 and x2. Once an EventML program type checks and is sane, it can finally be processed into a list of Nuprl abstractions, well-formedness lemmas, and programmability lemmas (meaning that given an event class, there exists a program that computes what the class observes). For each EventML declaration dec the interpreter generates (at least) an abstraction (i.e., a new Nuprl definition) and a well-formedness statement based on the type generated by the EventML type inferencer for dec Programmability lemmas are only generated for class declarations.

The EventML tool is a stand-alone tool, i.e., a source archive can be downloaded and installed on linux machines. EventML has also been fully integrated into Nuprl, i.e., Nuprl provides an easy access to EventML's Emacs interface and is able to load EventML's outputs. However, currently the only way to extract a (distributed) program from an EventML specification is to extract, in Nuprl, a program from the proof of some programmability lemma generated by EventML. Extracted programs are Nuprl terms which can be evaluated using any of our ML evaluators.

Type Error Slicing

EventML uses a type error slicing machinery [4, 5, 9] to report type errors as well as to report syntax errors. A type error in an untypable piece of code is defined as a location set in the piece of code that contains all and only the information necessary to fix the error, i.e., the parts of the code where changes can be made to fix the code, leaving out the parts where changes cannot fix the error. Such a location set is called a slice and is guaranteed (it is at this stage only a conjecture because no formal proof has yet been provided) to contain the user programming error. We have an Emacs interface that highlights slices directly in the source code.

References

[1] Stuart F. Allen, Mark Bickford, Robert L. Constable, Richard Eaton, Christoph Kreitz, Lori Lorigo, and E. Moran. Innovations in computational type theory using nuprl. J. Applied Logic, 4(4):428-469, 2006.

[2] Mark Bickford. Component specification using event classes. In Grace A. Lewis, Iman Poernomo, and Christine Hofmeister, editors, CBSE, volume 5582 of Lecture Notes in Computer Science, pages 140-155. Springer, 2009.

[3] Mark Bickford and Robert L. Constable. Formal foundations of computer security. In NATO Science for Peace and Security Series, D: Information and Communication Security, volume 14, pages 29-52. 2008.

[4] Christian Haack and J. B. Wells. Type error slicing in implicitly typed higher-order languages. In Pierpaolo Degano, editor, ESOP, volume 2618 of LNCS, pages 284-301. Springer, 2003.

[5] Christian Haack and J. B. Wells. Type error slicing in implicitly typed higher-order languages. Science of Computer Programming, 50(1-3):189-224, 2004.

[6] Martin Odersky, Martin Sulzmann, and Martin Wehr. Type inference with constrained types. Theor. Pract. Object Syst., 5(1):35-55, 1999.

[7] François Pottier. A modern eye on ML type inference: old techniques and recent developments. Lecture notes for the APPSEM Summer School, September 2005.

[8] François Pottier and Didier Rémy. The essence of ML type inference. In Benjamin C. Pierce, editor, Advanced Topics in Types and Program- ming Languages, chapter 10, pages 389-489. MIT Press, 2005.

[9] Vincent Rahli. Investigations in intersection types: Confluence, and semantics of expansion in the λ-calculus, and a type error slicing method. PhD thesis, Heriot-Watt University, January 2011.