| | Who Cites ring? |
|
| ring | Def ring(R;in;out)
Def == ( i:|R|. i:|R|.
Def == (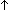 (R(source(in(i)))) & (R(source(in(i)))) & 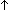 (R(destination(out(i)))) (R(destination(out(i))))
Def == (& source(out(i)) = i
Def == (& & destination(in(i)) = i
Def == (& & in(destination(out(i))) = out(i) 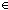 IdLnk IdLnk
Def == (& & out(source(in(i))) = in(i) 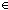 IdLnk) IdLnk)
Def == & ( i,j:|R|. i,j:|R|. 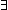 k: k: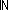 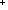 . . 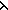 x.destination(out(x))^k(i) = j x.destination(out(x))^k(i) = j 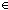 Id) Id)
Def == & |R| |
| | | Thm*  R:(Id R:(Id 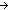 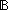 ), in,out:(|R| ), in,out:(|R| 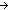 IdLnk). ring(R;in;out) IdLnk). ring(R;in;out) 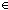 Prop Prop |
|
| rset | Def |R| == {i:Id| 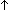 (R(i)) } (R(i)) } |
| | | Thm*  R:(Id R:(Id 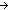 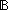 ). |R| ). |R| 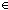 Type Type |
|
| ldst | Def destination(l) == 1of(2of(l)) |
| | | Thm*  l:IdLnk. destination(l) l:IdLnk. destination(l) 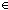 Id Id |
|
| fun_exp | Def f^n == primrec(n;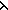 x.x; x.x;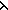 i,g. f o g) i,g. f o g) |
| | | Thm*  T:Type, n: T:Type, n: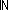 , f:(T , f:(T 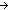 T). f^n T). f^n 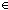 T T 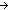 T T |
|
| IdLnk | Def IdLnk == Id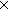 Id Id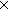 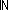 |
| | | Thm* IdLnk 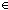 Type Type |
|
| Id | Def Id == Atom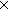 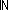 |
| | | Thm* Id 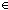 Type Type |
|
| nat_plus | Def 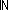 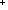 == {i: == {i: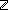 | 0<i } | 0<i } |
| | | Thm* 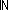 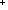 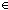 Type Type |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l) 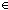 Id Id |
|
| assert | Def 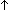 b == if b b == if b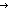 True else False fi True else False fi |
| | | Thm*  b: b: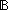 . b . b 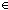 Prop Prop |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A 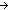 Type), p:(a:A Type), p:(a:A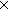 B(a)). 2of(p) B(a)). 2of(p) 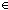 B(1of(p)) B(1of(p)) |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A 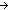 Type), p:(a:A Type), p:(a:A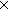 B(a)). 1of(p) B(a)). 1of(p) 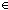 A A |
|
| compose | Def (f o g)(x) == f(g(x)) |
| | | Thm*  A,B,C:Type, f:(B A,B,C:Type, f:(B 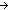 C), g:(A C), g:(A 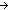 B). f o g B). f o g 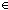 A A 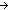 C C |
|
| primrec | Def primrec(n;b;c) == if n=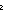 0 0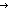 b else c(n-1,primrec(n-1;b;c)) fi (recursive) b else c(n-1,primrec(n-1;b;c)) fi (recursive) |
| | | Thm*  T:Type, n: T:Type, n: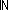 , b:T, c:( , b:T, c:(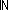 n n 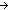 T T 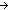 T). primrec(n;b;c) T). primrec(n;b;c) 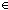 T T |
|
| nat | Def 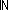 == {i: == {i: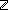 | 0 | 0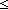 i } i } |
| | | Thm* 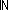 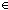 Type Type |
|
| eq_int | Def i=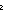 j == if i=j j == if i=j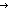 true true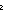 ; false ; false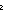 fi fi |
| | | Thm*  i,j: i,j: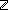 . (i= . (i=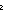 j) j) 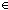 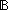 |
|
| le | Def A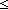 B == B == 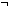 B<A B<A |
| | | Thm*  i,j: i,j: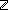 . (i . (i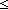 j) j) 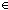 Prop Prop |
|
| not | Def 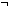 A == A A == A 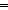 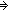 False False |
| | | Thm*  A:Prop. ( A:Prop. (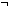 A) A) 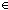 Prop Prop |