| Rank | Theorem | Name |
| 21 | Thm*  a:{2...}, b: a:{2...}, b: , g,h:({a..b , g,h:({a..b } }   ). ).
Thm* is_prime_factorization(a; b; g)
Thm*  
Thm* is_prime_factorization(a; b; h)     {a..b {a..b }(g) = }(g) =   {a..b {a..b }(h) }(h)   g = h g = h | [prime_factorization_unique] |
| cites the following: |
| 19 | Thm*  a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
Thm* is_prime_factorization(a; b; f)
Thm*  
Thm* prime(p)   p | p |   {a..b {a..b }(f) }(f)   p p 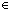 {a..b {a..b } & 0<f(p) } & 0<f(p) | [prime_factorization_includes_prime_divisors] |
| 7 | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. 0<f(j) }. 0<f(j)   j | j |   {a..b {a..b }(f) }(f) | [factor_divides_evalfactorization] |
| 20 | Thm*  a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
Thm* is_prime_factorization(a; b; f)
Thm*  
Thm* prime(p)
Thm*  
Thm* p |   {a..b {a..b }(f) }(f)     {a..b {a..b }(f) = p }(f) = p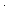   {a..b {a..b }(reduce_factorization(f; p)) }(reduce_factorization(f; p)) | [remove_prime_factor] |
| 0 | Thm*  a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ), j:{a..b ), j:{a..b }. }.
Thm* 0<f(j)
Thm*  
Thm* 0<g(j)   reduce_factorization(f; j) = reduce_factorization(g; j) reduce_factorization(f; j) = reduce_factorization(g; j)   f = g f = g | [reduce_factorization_cancel] |
| 4 | Thm*  a: a: 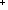 , b: , b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) }(f) 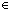  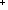 | [eval_factorization_nat_plus] |
| 7 | Thm*  a: a: 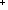 , b: , b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
Thm* 2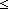 j j   0<f(j) 0<f(j)     {a..b {a..b }(reduce_factorization(f; j))< }(reduce_factorization(f; j))<  {a..b {a..b }(f) }(f) | [eval_reduce_factorization_less] |
| 1 | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
Thm* 0<f(j)
Thm*  
Thm* is_prime_factorization(a; b; f)
Thm*  
Thm* is_prime_factorization(a; b; reduce_factorization(f; j)) | [reduce_fac_pres_isprimefac] |
| 6 | Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 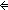  f = ( f = (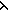 x.0) x.0) | [eval_factorization_one_c] |
| 6 | Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 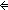  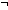 ( (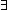 i:{a..b i:{a..b }. 0<f(i)) }. 0<f(i)) | [eval_factorization_one_b] |