So, we are down to proving

(A) z:{a...}, m:{a...z-1}, s1:({a...m}{1...n}Peg),
(A) s2:({m+1...z}{1...n}Peg).
(A) (s1 @(m) s2) is a Hanoi(n disk) seq on a..z
(A) & s1(a) = (i.p)
(A) & s2(z) = (i.q)

Since p  q, otherPeg(p; q) is the remaining Peg. The stacking situation i.otherPeg(p; q) has all it disks on that other Peg. Application of the inductive hypothesis twice assures us there a Hanoi sequence moving the disks smaller than n from peg p to otherPeg(p; q) as well as another one from otherPeg(p; q) to q. Applying it first using p, otherPeg(p; q)  Peg, a  , gives us m  {a...} and s1  {a...m}{1...n-1}Peg such that

s1 is a Hanoi(n-1 disk) seq on a..m

s1(a) = (i.p)

s1(m) = (i.otherPeg(p; q))

Applying the inductive hypothesis further to otherPeg(p; q), q  Peg, m+1   gives us z  {m+1...} and s2  {m+1...z}{1...n-1}Peg such that

s2 is a Hanoi(n-1 disk) seq on m+1..z

s2(m+1) = (i.otherPeg(p; q))

s2(z) = (i.q)

The principle for showing how to combine two such Hanoi sequences to show our goal has been isolated in a lemma:

Thm*  n:, a:, z:{a...}, m:{a...z-1}, f,g:({1...n}Peg).
Thm*  f(n)  g(n)
Thm*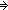  
Thm*  (s1:({a...m}{1...n-1}Peg), s2:({m+1...z}{1...n-1}Peg).
Thm*  (s1 is a Hanoi(n-1 disk) seq on a..m
Thm*  (& s1(a) = f  {1...n-1}Peg
Thm*  (& s2 is a Hanoi(n-1 disk) seq on m+1..z
Thm*  (& s2(z) = g  {1...n-1}Peg
Thm*  (& s1(m) = s2(m+1)
Thm*  (& (i:{1...n-1}. s1(m,i)  f(n) & s2(m+1,i)  g(n)))
Thm*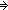  
Thm*  (r1:({a...m}{1...n}Peg), r2:({m+1...z}{1...n}Peg).
Thm*  ((r1 @(m) r2) is a Hanoi(n disk) seq on a..z & r1(a) = f & r2(z) = g)

Gloss

Applying this special lemma here to show (A) from above, reduces to establishing that for i  {1...n-1}

s1(m,i)  p, which follows from s1(m) = (i.otherPeg(p; q)) above, and

s2(m+1,i)  q, which follows from s2(m+1) = (i.otherPeg(p; q)) above.

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html