Thm* Y(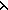 f,x. if x= f,x. if x=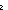 0 0 1 else x 1 else x f(x-1) fi) f(x-1) fi)      | [sfa_doc_ycomb_factorial_typing] |
Thm* (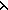 f,x. if x= f,x. if x=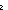 0 0 1 else x 1 else x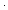 f(x-1) fi) f(x-1) fi)  ( (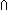 k: k: . ( . ( k k   ) )   (k+1) (k+1)   ) ) | [sfa_doc_factbody_polytyping] |
Thm* (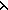 x.x) = ( x.x) = (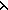 x.if x<0 x.if x<0 0 ; x fi) 0 ; x fi)      | [sfa_doc_funeq_example1] |
Thm* (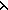 n.n< n.n<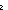 0) = ( 0) = (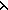 n.false n.false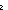 ) )     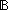 | [sfa_doc_sqtype_ctr_example_part2] |
Thm*  x: x: . . 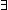 y: y: . y . y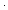 y y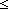 x & x<(y+1) x & x<(y+1)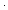 (y+1) (y+1) | [sfa_doc_nat_sqrt] |
Thm*  A:Type, a:A, e:(A A:Type, a:A, e:(A  A), i: A), i: . i steps of e from a . i steps of e from a  A A | [sfa_doc_sequence_rel_wf] |
Thm* (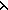 x.Case of x x.Case of x
Thm* ( x.Canil x.Canil  0 0
Thm* ( x.Cau.v, rec:r x.Cau.v, rec:r  InjCase(if u<r InjCase(if u<r inl(*) ; inr( inl(*) ; inr(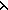 .*) fi; a. r; b. u+1)) .*) fi; a. r; b. u+1))
Thm* =
Thm* ext{sfa_doc_find_small_greater_bound}
Thm*  ( (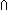 k: k: . x:( . x:( k List) k List)  {y: {y: (k+1)| y greater-bounds x }) (k+1)| y greater-bounds x }) | [sfa_doc_find_small_greater_bound_extr_eq] |
Thm* (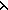 k,x. k) k,x. k)
Thm* =
Thm* ext{sfa_doc_find_greater_bound_stupidly}
Thm*  k: k:   x:( x:( k List) k List)  {y: {y: (k+1)| y greater-bounds x } (k+1)| y greater-bounds x } | [sfa_doc_find_greater_bound_stupidly_extr_eq] |
Thm* k:   x:( x:( k List) k List)  {y: {y: (k+1)| y greater-bounds x } (k+1)| y greater-bounds x } | [sfa_doc_find_greater_bound_stupidly] |
Thm* 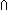 k: k: . x:( . x:( k List) k List)  {y: {y: (k+1)| y greater-bounds x } (k+1)| y greater-bounds x } | [sfa_doc_find_small_greater_bound] |
Thm*  f,g:( f,g:(    ). ).
Thm* (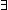 x: x: . f zero beyond x) & ( . f zero beyond x) & (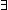 x: x: . g zero beyond x) . g zero beyond x)
Thm*  
Thm* (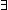 x: x: . ( . (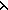 i.if i even i.if i even f(i) else g(i) fi) zero beyond x) f(i) else g(i) fi) zero beyond x) | [sfa_doc_alternate_zero_beyond] |
Thm*  a,b: a,b: . max(a;b) . max(a;b)   | [sfa_doc_max_int_wf] |
Thm*  x: x: , f:( , f:(    ). f zero beyond x ). f zero beyond x  Prop Prop | [sfa_doc_props_as_types_example1_wf] |
Thm* P 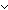 Q Q   ( (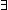 x: x: . (x = 0 . (x = 0   P) & (x P) & (x 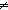 0 0   Q)) Q)) | [sfa_doc_or_dec] |
Thm*  f:( f:(    ). ).
Thm* ( n: n: . f(n) = 0) . f(n) = 0)
Thm*  
Thm* ( n: n: . if f(n)= . if f(n)=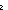 0 0 False else False else  C:Prop{1}. C fi) C:Prop{1}. C fi)  Prop{1} Prop{1} | [sfa_doc_predicativity_sample8] |
Thm*  A:Type, P:(A A:Type, P:(A  Prop), n: Prop), n: , X:(A^n). ( , X:(A^n). (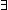 u in X: A^n. P(u)) u in X: A^n. P(u))  Prop Prop | [sfa_doc_ntuple_contains_wf] |
Thm*  n: n: . n . n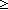 2 2   (A^n) = A (A^n) = A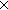 (A^(n-1)) (A^(n-1)) | [sfa_doc_ntuple_is_prod] |
Thm*  A:Type, n: A:Type, n: . (A^n) . (A^n)  Type Type | [sfa_doc_ntuple_wf] |
Thm*  x:{x: x:{x: | (x rem 2) = 0 }. x! | (x rem 2) = 0 }. x!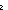   | [sfa_doc_factorial2_wf] |
Thm*  x: x: . x! . x!   | [sfa_doc_factorial_wf] |
Thm*  k: k: . 0<k & (2 . 0<k & (2 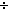 k)<1 k)<1   2<k 2<k | [sfa_doc_cand_example] |
Thm*  f:{f:( f:{f:(   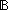 )| )| 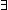 x: x: . f(x) }, i: . f(x) }, i: . i<mu(f) . i<mu(f)   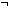 f(i) f(i) | [kleene_minimize_is_lb] |
Thm*  f:{f:( f:{f:(   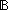 )| )| 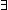 x: x: . f(x) }. f(mu(f)) . f(x) }. f(mu(f)) | [kleene_minimize_is_fp] |
Thm* mu  {f:( {f:(   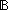 )| )| 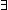 x: x: . f(x) } . f(x) }   | [kleene_minimize_wf] |
Thm*  f:{f:( f:{f:(   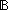 )| )| 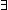 x: x: . f(x) }. . f(x) }. 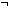 f(0) f(0)   ( (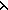 x.f(1+x)) x.f(1+x))  {f:( {f:(   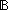 )| )| 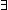 x: x: . f(x) } . f(x) } | [kleene_tail] |
Def f zero beyond x ==  y: y: . x<y . x<y   f(y) = 0 f(y) = 0   | [sfa_doc_props_as_types_example1] |
Def sfa_doc_oparm_sample{2:n}(A) == A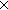  | [sfa_doc_oparm_sample2] |
Def sfa_doc_oparm_sample{1:n}(A) ==    A A | [sfa_doc_oparm_sample1] |
Def Induction for x: . P(x) == P(0) & ( . P(x) == P(0) & ( x: x: . P(x) . P(x)   P(x+1)) P(x+1))   ( ( x: x: . P(x)) . P(x)) | [sfa_doc_indscheme] |
Def 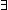 u in X: A^n. P(u) u in X: A^n. P(u)
Def == n = 1   & P(X) & P(X) 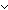 n n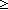 2 & (X/a,rest. P(a) 2 & (X/a,rest. P(a) 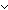 ( (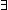 u in rest: A^(n-1). P(u))) u in rest: A^(n-1). P(u)))
Def (recursive) | [sfa_doc_ntuple_contains] |