| | Some definitions of interest. |
|
| nat_plus | Def  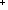 == {i: == {i: | 0<i } | 0<i } |
| | | Thm*  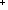  Type Type |
|
| nequal | Def a 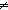 b b  T == T == 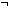 a = b a = b  T T |
| | | Thm*  A:Type, x,y:A. (x A:Type, x,y:A. (x 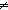 y) y)  Prop Prop |
|
| sfa_doc_sexpr | Def Sexpr(A) == rec(T.(T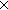 T)+A) T)+A) |
| | | Thm*  A:Type. Sexpr(A) A:Type. Sexpr(A)  Type Type |
|
| sfa_doc_sexpr_cdr | Def sexprCdr(s) == Case of s : Inj(x)  Inj(x) ; Cons(s1;s2) Inj(x) ; Cons(s1;s2)  s2 s2 |
| | | Thm*  A:Type, s:Sexpr(A). sexprCdr(s) A:Type, s:Sexpr(A). sexprCdr(s)  Sexpr(A) Sexpr(A) |
|
| sfa_doc_sexpr_size | Def Size(s) == Case of s : Inj(x)  1 ; Cons(s1;s2) 1 ; Cons(s1;s2)  Size(s1)+Size(s2) Size(s1)+Size(s2)
Def (recursive) |
| | | Thm*  A:Type, s:Sexpr(A). Size(s) A:Type, s:Sexpr(A). Size(s)   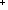 |