Sequents with Type Conclusions - continued from Sequents

A type expression may be used as the conclusion of a sequent, and the sequent is considered true just when there is some "witness" expression, say "???", that would make the sequent true if the conclusion, say "T", were replaced by "???  T". For example,

1. x :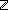 
2. y :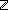 
3. x+1<y
  {z:| x<z & z<y }

is true because, for example,

1. x :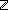 
2. y :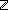 
3. x+1<y
  y-1  {z:| x<z & z<y }

While there is a proof rule for providing such a witness explicitly to justify such a sequent, it is common to defer or avoid explicitly supplying such witnesses. For example, one may infer

  x:AB(x) from

  A  Type, and

1. x : A    B(x)

since we can construct a witness "x.b" for the goal from a witness "b" for the last subgoal. Similarly, we can infer "  AB" from "  A" and "  B", since a witness <a,b> can be constructed from witnesses for the subgoals. An example of a proof that defers witness specification is

Thm* x:( List){y:| y greater-bounds x }

The proof proceeds by induction on lists, specifying witnesses explicitly at three key points. It provides -3 as a value on the empty list, and for the (u.v) case (under the inductive hypothesis) it specifies using either a value w assumed to work for sublist v, or u+2, depending on whether u<w.

The proof does not explicitly show a member of x:( List){y:| y greater-bounds x }. It is simply argued that such a member can be constructed.

There are three lines of further elaboration at this point, and there is some interaction between them.

Proof Witness Extraction is a method for actually extracting a witness from the proof of a type-conclusioned sequent.

Sequents with Restricted Declarations are introduced to allow us to assert the independence of witnesses from certain variables. (1. x : A  [not for witness]  <sequent>)

Propositional Proof Witness Extraction is extracting from proofs of propositions certain kinds of witnesses inherent in their constructive meaning, this being effected by representing Propositions as Types

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html