| 1 | 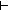 Bij(St; x,y:Alph*//(x LangOf(Auto)-induced Equiv y); f)
& ( Bij(St; x,y:Alph*//(x LangOf(Auto)-induced Equiv y); f)
& ( s:St, a:Alph. f( s:St, a:Alph. f(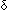 Auto(s,a)) = a.f(s) Auto(s,a)) = a.f(s) 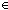 x,y:Alph*//(x LangOf(Auto)-induced Equiv y))
& f(InitialState(Auto)) = nil x,y:Alph*//(x LangOf(Auto)-induced Equiv y))
& f(InitialState(Auto)) = nil 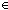 x,y:Alph*//(x LangOf(Auto)-induced Equiv y)
& ( x,y:Alph*//(x LangOf(Auto)-induced Equiv y)
& ( s:St. FinalState(Auto)(s) = Auto(f(s)) s:St. FinalState(Auto)(s) = Auto(f(s))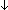 ) ) |
| 2 | 10. f1: St 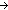 (x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) (x,y:Alph*//(x LangOf(Auto)-induced Equiv y))
11. s: St
12. a: Alph
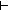 a.f1(s) a.f1(s) 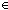 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) |
| 3 | 10. f1: St 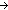 (x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) (x,y:Alph*//(x LangOf(Auto)-induced Equiv y))
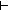 nil nil 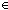 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) |
| 4 | 10. f1: St 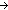 (x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) (x,y:Alph*//(x LangOf(Auto)-induced Equiv y))
11. s: St
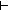 Auto(f1(s)) Auto(f1(s))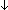 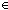 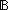 |