| 1 | 10. l: {l:(Alph*)| ||l|| = t }
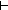 LangOf(Auto) LangOf(Auto) 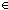 Alph* Alph* 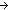 Prop Prop |
| 2 | 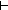 Fin({l:(Alph*)| ||l|| = t }) Fin({l:(Alph*)| ||l|| = t }) |
| 3 | 10. t1: {l:(Alph*)| ||l|| = t }
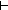 Dec(( Dec((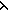 l.LangOf(Auto)(l))(t1)) l.LangOf(Auto)(l))(t1)) |
| 4 | 10. Dec(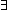 t:{l:(Alph*)| ||l|| = t }. ( t:{l:(Alph*)| ||l|| = t }. (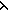 l.LangOf(Auto)(l))(t)) l.LangOf(Auto)(l))(t))
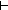 Dec( Dec(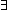 l:{l:(Alph*)| ||l|| = t }. LangOf(Auto)(l)) l:{l:(Alph*)| ||l|| = t }. LangOf(Auto)(l)) |