| 1 | 11. RL: S.car*
12. 0 < ||RL||
13. ||RL||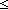 n-1+1 n-1+1
14. RL[(||RL||-1)] = si
15. ||RL|| = n-1+1
16.  i: i: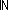 ||RL||, j: ||RL||, j: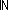 i. i.  RL[i] = RL[j] RL[i] = RL[j]
17.  s:S.car. mem_f(S.car;s;RL) s:S.car. mem_f(S.car;s;RL)   ( ( w:Alph*. (S:w w:Alph*. (S:w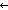 si) = s) si) = s)
18.  k: k: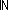 .
k .
k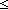 nn nn   (
( RLa:S.car*.
( RLa:S.car*.
( i:{1..||RL|| i:{1..||RL|| }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) 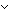 mem_f(S.car;S.act(a,RL[i]);RLa))
& ( mem_f(S.car;S.act(a,RL[i]);RLa))
& ( a:Alph. g(a) < k a:Alph. g(a) < k   mem_f(S.car;S.act(a,hd(RL));RL) mem_f(S.car;S.act(a,hd(RL));RL) 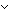 mem_f(S.car;S.act(a,hd(RL));RLa))
& ( mem_f(S.car;S.act(a,hd(RL));RLa))
& ( s:S.car. mem_f(S.car;s;RLa) s:S.car. mem_f(S.car;s;RLa)   ( ( w:Alph*. (S:w w:Alph*. (S:w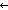 si) = s))) si) = s)))
19. RLa: S.car*
20.  i:{1..||RL|| i:{1..||RL|| }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) 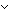 mem_f(S.car;S.act(a,RL[i]);RLa) mem_f(S.car;S.act(a,RL[i]);RLa)
21.  a:Alph. g(a) < nn a:Alph. g(a) < nn   mem_f(S.car;S.act(a,hd(RL));RL) mem_f(S.car;S.act(a,hd(RL));RL) 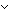 mem_f(S.car;S.act(a,hd(RL));RLa) mem_f(S.car;S.act(a,hd(RL));RLa)
22.  s:S.car. mem_f(S.car;s;RLa) s:S.car. mem_f(S.car;s;RLa)   ( ( w:Alph*. (S:w w:Alph*. (S:w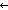 si) = s) si) = s)
23. La': S.car*
24.  t:S.car. mem_f(S.car;t;RLa) t:S.car. mem_f(S.car;t;RLa)   mem_f(S.car;t;RL) mem_f(S.car;t;RL) 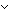 mem_f(S.car;t;La') mem_f(S.car;t;La')
25.  t:S.car. mem_f(S.car;t;La') t:S.car. mem_f(S.car;t;La')   mem_f(S.car;t;RLa) mem_f(S.car;t;RLa)
26. La' = nil
27. y: {x:(S.car*)| 0 < ||x|| & ||x||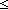 n+1 } n+1 }
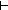 0 0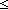 ||y||-1 ||y||-1 |