| | Some definitions of interest. |
|
| next_nat_pair | Def next_nat_pair(xy) == xy/x,y. if y= 0 0 <0,x+1> else <x+1,y-1> fi <0,x+1> else <x+1,y-1> fi |
| | | Thm* next_nat_pair          |
|
| prev_nat_pair | Def prev_nat_pair(xy) == xy/x,y. if x= 0 0 <y-1,0> else <x-1,y+1> fi <y-1,0> else <x-1,y+1> fi |
| | | Thm* prev_nat_pair  {xy:( {xy:(   )| )|  xy = <0,0> xy = <0,0>     } }     |
|
| eq_int | Def i= j == if i=j j == if i=j true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: . (i= . (i= j) j)   |
|
| nat | Def  == {i: == {i: | 0 | 0 i } i } |
| | | Thm*   Type Type |
|
| nequal | Def a 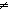 b b  T == T ==  a = b a = b  T T |
| | | Thm*  A:Type, x,y:A. (x A:Type, x,y:A. (x 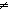 y) y)  Prop Prop |