Selected Objects
| Introduction | Introductory Remarks |
| def | is_one_one_corr_rel
|
One-one correlation as a relation
1-1-Corr x:A,y:B. R(x;y) == ( x:A. x:A.  !y:B. R(x;y)) & ( !y:B. R(x;y)) & ( y:B. y:B.  !x:A. R(x;y)) !x:A. R(x;y)) |
| def | is_list_mem
|
(a is a member of list xs)
a  xs == Case of xs; nil xs == Case of xs; nil  False ; x.ys False ; x.ys  a = x a = x  A A 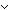 (a (a  ys) (recursive) ys) (recursive) |
| THM | ndiff_vs_diff
|
 a,b: a,b: . a . a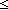 b b   (b -- a) = b-a (b -- a) = b-a |
| THM | eq_int_is_eq_nsub
|
IsEqFun( b; b;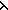 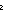 i,j. i= i,j. i=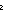 j) j) |
| THM | decidable__nat_equal
|
 i,j: i,j: . Dec(i = j) . Dec(i = j) |
| THM | exteq_singleton_vs_intseg
|
 a,a': a,a': . a'-a = 1 . a'-a = 1   ({a..a' ({a..a' } =ext {a: } =ext {a: }) }) |
| THM | exteq_prod_family_singleton_vs_intseg
|
 a,a': a,a': . .
a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type{i}). (i:{a..a' Type{i}). (i:{a..a' } }  B(i)) =ext ({a: B(i)) =ext ({a: } }  B(a))) B(a))) |
| THM | exteq_sum_family_singleton_vs_intseg
|
 a,a': a,a': . .
a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type{i}). (i:{a..a' Type{i}). (i:{a..a' } } B(i)) =ext ({a: B(i)) =ext ({a: } } B(a))) B(a))) |
| def | injection_type
|
(the injections from A into B)
A inj B == {f:(A B == {f:(A  B)| Inj(A; B; f) } B)| Inj(A; B; f) } |
| def | bijection_type
|
(the bijections from A onto B)
A bij B == {f:(A B == {f:(A  B)| Bij(A; B; f) } B)| Bij(A; B; f) } |
| THM | injtype_vs_inj
|
(  (A inj (A inj B)) B))   ( ( f:(A f:(A  B). Inj(A; B; f)) B). Inj(A; B; f)) |
| THM | injection_type_fun
|
 f:(A inj f:(A inj B). f B). f  A A  B B |
| THM | injection_type_injection
|
 f:(A inj f:(A inj B). Inj(A; B; f) B). Inj(A; B; f) |
| THM | inj_point_deletion
|
 f:(A inj f:(A inj B), a:A. f B), a:A. f  {x:A| {x:A|  x = a } x = a }  {y:B| {y:B|  y = f(a) } y = f(a) } |
| THM | inj_point_deletion_inj
|
 f:(A inj f:(A inj B), a:A. f B), a:A. f  {x:A| {x:A|  x = a } inj x = a } inj {y:B| {y:B|  y = f(a) } y = f(a) } |
| THM | inj_from_empty_unique
|
 ( (  A) A)   ( ( ! ! (A inj (A inj B)) B)) |
| THM | bijtype_sub_injtype
|
(A bij B) B) 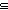 (A inj (A inj B) B) |
| THM | bijection_type_inc_inj
|
(A bij B) B) 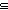 (A inj (A inj B) B) |
| THM | nsub_inj_lop_typing
|
 a: a: 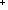 , b: , b: , f:( , f:( a inj a inj  b). f b). f   (a-1) inj (a-1) inj {x: {x: b| b|  x = f(a-1) } x = f(a-1) } |
| THM | nsub_inj_fill_typing
|
 a: a: 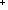 , b: , b: , j: , j: b, f:( b, f:( (a-1) inj (a-1) inj {x: {x: b| b|  x = j }). x = j }).
(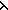 i.if i= i.if i=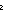 a-1 a-1 j else f(i) fi) j else f(i) fi)   a inj a inj  b b |
| def | surjection_type
|
(the surjections from A onto B)
A onto B == {f:(A B == {f:(A  B)| Surj(A; B; f) } B)| Surj(A; B; f) } |
| THM | bijtype_sub_surjtype
|
(A bij B) B) 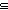 (A onto (A onto B) B) |
| THM | bijection_type_inc_surj
|
(A bij B) B) 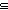 (A onto (A onto B) B) |
| THM | bijtype_exteq_inj_isect_surjtype
|
(A bij B) =ext ((A inj B) =ext ((A inj B) B)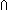 (A onto (A onto B)) B)) |
| COM | unicomp_assoc
|
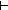 h o g o f = h o g o f
... h o g o f = h o g o f
... |
| COM | inverse_function_intro
|
Explain inverse functions and
Def InvFuns(A; B; f; g) == g o f = Id & f o g = Id |
| COM | one_one_corr_intro
|
One-to-One Correspondence
... |
| COM | one_one_corr_via_inverse
|
One-to-One Correspondence via Inverse Functions
... |
| COM | one_one_corr_intro_aux1
|
Comparison of definitional resources used.
... |
| COM | one_one_corr_intro3
|
One-to-One Correspondence: equivalence of two characterizations.
... |
| COM | count_demo
|
Counting is finding a function of a certain kind.
... |
| def | list_to_function
|
A function mapping positions in a list to entries
seq:l(i) == l[i] |
| COM | note_on_generalization_for_induction
|
Not done yet. |
| def | replace_fn_values
|
(Replace values x s.t. P(x) by y in f)(i) == if P(f(i)) y else f(i) fi y else f(i) fi |
| def | delete_fenum_value
|
Special purpose operation for shrinking the domain and range of an injection simultaneously. See REMARK.
Replace value k by f(m) in f == Replace values x s.t. x=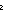 k by f(m) in f k by f(m) in f |
| COM | delete_fenum_value_example
|
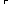 let xs = [1; 3; 0; 7; 2; 4; 6; 5] in let xs = [1; 3; 0; 7; 2; 4; 6; 5] in
 let v = 4 in (Replace value v by seq:xs(||xs||-1) in seq:xs){ let v = 4 in (Replace value v by seq:xs(||xs||-1) in seq:xs){ (||xs||-1)} (||xs||-1)}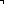
*
[1; 3; 0; 7; 2; 5; 6] |
| THM | delete_fenum_value_comp1_gen
|
Inj({u: | P(u) }; {u: | P(u) }; {u: | Q(u) }; f) | Q(u) }; f)
 
( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }, i:{u: | Q(v) }, i:{u: | P(u) & | P(u) &  u = m }. u = m }.
(f(i) = k   (Replace value k by f(m) in f)(i) = f(m) (Replace value k by f(m) in f)(i) = f(m)  {v: {v: | Q(v) & | Q(v) &  v = k }) v = k }) |
| THM | delete_fenum_value_comp2_gen
|
Inj({u: | P(u) }; {u: | P(u) }; {u: | Q(u) }; f) | Q(u) }; f)
 
( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }, i:{u: | Q(v) }, i:{u: | P(u) & | P(u) &  u = m }. u = m }.
( f(i) = k f(i) = k   (Replace value k by f(m) in f)(i) = f(i) (Replace value k by f(m) in f)(i) = f(i)  {v: {v: | Q(v) & | Q(v) &  v = k }) v = k }) |
| THM | delete_fenum_value_is_inj_genW
|
Inj({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
 
( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
((Replace value k by f(m) in f)  {u: {u: | P(u) & | P(u) &  u = m } u = m }  {v: {v: | Q(v) & | Q(v) &  v = k } v = k }
(& Inj({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
(& Inj(Replace value k by f(m) in f)) |
| THM | delete_fenum_value_is_inj_gen
|
Inj({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
 
( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
(Inj({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
(Inj(Replace value k by f(m) in f)) |
| THM | delete_fenum_value_is_fenum_gen
|
Bij({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
 
( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
(Bij({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
(Bij(Replace value k by f(m) in f)) |
| THM | delete_fenum_value_comp1
|
Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
 
( i: i: m. f(i) = k m. f(i) = k   (Replace value k by f(m) in f)(i) = f(m) (Replace value k by f(m) in f)(i) = f(m)   k) k) |
| THM | delete_fenum_value_comp2
|
Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
 
( i: i: m. m.  f(i) = k f(i) = k   (Replace value k by f(m) in f)(i) = f(i) (Replace value k by f(m) in f)(i) = f(i)   k) k) |
| THM | delete_fenum_value_is_inj
|
Inj( (m+1); (m+1);  (k+1); f) (k+1); f)   Inj( Inj( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) |
| THM | delete_fenum_value_is_fenum
|
Bij( (m+1); (m+1);  (k+1); f) (k+1); f)   Bij( Bij( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) |
| THM | finite_inj_counter_example
(Proof Gloss) |
Lemma for the pigeon-hole principle.
A finite non-injection into integers maps some two distinct arguments to the same value.
 m: m: , f:( , f:( m m   ). ).  Inj( Inj( m; m;  ; f) ; f)   ( ( x: x: m, y: m, y: x. f(x) = f(y)) x. f(x) = f(y)) |
| THM | inj_imp_le
(Proof Gloss) |
The range of a finite injection is as big as its domain.
( f:( f:( m m   k). Inj( k). Inj( m; m;  k; f)) k; f))   m m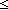 k k |
| THM | inj_typing_imp_le
|
The range of a finite injection is as big as its domain.
(  ( ( m inj m inj  k)) k))   m m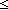 k k |
| THM | inj_imp_le2
|
The range of a finite injection is as big as its domain.
 m,k: m,k: , f:( , f:( m m   k). Inj( k). Inj( m; m;  k; f) k; f)   m m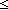 k k |
| THM | pigeon_hole
(Proof Gloss) |
The pigeon-hole principle
A mapping from one finite collection into a smaller collection assigns a single output to two inputs.
 m,k: m,k: , f:( , f:( m m   k). k<m k). k<m   ( ( x,y: x,y: m. x m. x 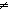 y & f(x) = f(y)) y & f(x) = f(y)) |
| def | rel_1_1
|
(R is a 1-1 relation)
R is 1-1 ==  x,x':A, y,y':B. R(x,y) & R(x',y') x,x':A, y,y':B. R(x,y) & R(x',y')   (x = x' (x = x'   y = y') y = y') |
| def | rel_1_1_b
|
(R(x;y) is a 1-1 relation in x in A and y in B)
1-1 x A,y A,y B. R(x;y) == B. R(x;y) ==  x,x':A, y,y':B. R(x;y) & R(x';y') x,x':A, y,y':B. R(x;y) & R(x';y')   (x = x' (x = x'   y = y') y = y') |
| THM | rel_1_1_eq_rel_1_1_b
|
Equivalence of two forms of relational one-to-one correspondence
 R:(A R:(A  B B  Prop). (R is 1-1) = (1-1 x Prop). (R is 1-1) = (1-1 x A,y A,y B. R(x;y)) B. R(x;y)) |
| def | inv_funs_2
|
(f and g are inverse functions, i.e. they cancel each other)
InvFuns(A;B;f;g) == ( x:A. g(f(x)) = x) & ( x:A. g(f(x)) = x) & ( y:B. f(g(y)) = y) y:B. f(g(y)) = y) |
| THM | inv_funs_2_identity
|
InvFuns(A;A;Id;Id) |
| def | one_one_corr_2
|
(types A and B are in one-to-one corresponence)
A ~ B ==  f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g) |
| THM | one_one_corr_2_functionality_wrt_eq
|
A = A'   B = B' B = B'   (A ~ B) = (A' ~ B') (A ~ B) = (A' ~ B') |
| THM | fun_with_inv2_is_inj
(Proof Gloss) |
InvFuns(A;B;f;g)   Inj(A; B; f) Inj(A; B; f) |
| THM | fun_with_inv2_is_surj
(Proof Gloss) |
InvFuns(A;B;f;g)   Surj(A; B; f) Surj(A; B; f) |
| THM | sq_stable__inv_funs_2
|
 f:(A f:(A  B), g:(B B), g:(B  A). SqStable(InvFuns(A;B;f;g)) A). SqStable(InvFuns(A;B;f;g)) |
| def | compose_iter
|
Iterated self-composition of a function.
f{ i}(x) == if i= i}(x) == if i=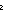 0 0 x else f(f{ x else f(f{ i-1}(x)) fi (recursive) i-1}(x)) fi (recursive) |
| def | least
|
(the least number i such that p(i))
least i: . p(i) == if p(0) . p(i) == if p(0) 0 else (least i: 0 else (least i: . p(i+1))+1 fi (recursive) . p(i+1))+1 fi (recursive) |
| THM | least_characterized
|
Characterization of "least".
 k: k: , p:{p:( , p:{p:( k k  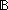 )| )|  i: i: k. p(i) }. k. p(i) }.
(least i: . p(i)) . p(i))  {i: {i: k| p(i) & ( k| p(i) & ( j: j: i. i.  p(j)) } p(j)) } |
| THM | least_characterized2
|
Characterization of "least".
 p:{p:( p:{p:(   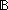 )| )|  i: i: . p(i) }. . p(i) }.
(least i: . p(i)) . p(i))  {i: {i: | p(i) & ( | p(i) & ( j: j: . j<i . j<i    p(j)) } p(j)) } |
| THM | least_satisfies
|
The least number having a property has it.
 k: k: , p:{p:( , p:{p:( k k  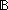 )| )|  i: i: k. p(i) }. p(least i: k. p(i) }. p(least i: . p(i)) . p(i)) |
| THM | least_is_least
|
No number smaller than the least one having a property has it.
 k: k: , p:{p:( , p:{p:( k k  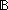 )| )|  i: i: k. p(i) }, j: k. p(i) }, j: (least i: (least i: . p(i)). . p(i)).  p(j) p(j) |
| THM | least_is_least2
|
No number smaller than the least one having a property has it.
 p:{p:( p:{p:(   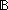 )| )|  i: i: . p(i) }, j: . p(i) }, j: (least i: (least i: . p(i)). . p(i)).  p(j) p(j) |
| THM | least_satisfies2
|
The least number having a property has it.
 p:{p:( p:{p:(   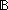 )| )|  i: i: . p(i) }. p(least i: . p(i) }. p(least i: . p(i)) . p(i)) |
| THM | nsub_discr_range_surj
|
(A Discrete)
 
( k: k: , f:( , f:( k k  A). A).
({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
(& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
(& Surj( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) |
| THM | nsub_discr_range_surjtype
|
(A Discrete)   ( ( k: k: , f:( , f:( k k  A). f A). f   k onto k onto {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) |
| THM | nsub_inj_discr_range_bij
|
(A Discrete)
 
( k: k: , f:( , f:( k inj k inj A). A).
({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
(& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
(& Bij( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) |
| THM | nsub_inj_discr_range_bijtype
|
Characterizing an injection as a bijection
(A Discrete)   ( ( k: k: , f:( , f:( k inj k inj A). f A). f   k bij k bij {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) |
| THM | nsub_surj_least_preimage_total_gen
|
Computing the inverse of a finite function
 e:(B e:(B  B B  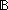 ). ).
IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. (least x: B), y:B. (least x: . (f(x)) e y) . (f(x)) e y)   a) a) |
| THM | nsub_surj_least_preimage_total
|
Computing the inverse of a finite function
 f:( f:( a onto a onto  b), y: b), y: b. (least x: b. (least x: . f(x)= . f(x)=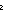 y) y)   a a |
| THM | nsub_surj_least_preimage_works_gen
|
 e:(B e:(B  B B  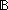 ). ).
IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. f(least x: B), y:B. f(least x: . (f(x)) e y) = y) . (f(x)) e y) = y) |
| THM | nsub_surj_least_preimage_works
|
 f:( f:( a onto a onto  b), y: b), y: b. f(least x: b. f(least x: . f(x)= . f(x)=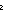 y) = y y) = y |
| def | find_first_iter
|
find_first_iter(v.p(v); v.f(v); a)
== if p(a) a else find_first_iter(v.p(v); v.f(v); f(a)) fi a else find_first_iter(v.p(v); v.f(v); f(a)) fi
(recursive) |
| THM | fin_plus_nat_ooc_nat
|
 k: k: . ( . ( k+ k+ ) ~ ) ~  |
| THM | nat_plus_ooc_nat
|
There are as many positive numbers as non-negative.
 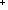 ~ ~  |
| def | is_finite_type
|
Finite(A) ==  n: n: . A ~ . A ~  n n |
| THM | nsub_is_finite
|
 k: k: . Finite( . Finite( k) k) |
| THM | ooc_preserves_finiteness
|
(A ~ B)   Finite(A) Finite(A)   Finite(B) Finite(B) |
| THM | no_finite_model_lemma
|
 R:(A R:(A  A A  Prop). Prop).
(  A) & (Trans x,y:A. R(x;y)) & ( A) & (Trans x,y:A. R(x;y)) & ( x:A. x:A.  y:A. R(x;y)) y:A. R(x;y))
 
( k: k: 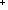 . .  f:( f:( k k  A). A).  i,j: i,j: k. i<j k. i<j   R(f(i);f(j))) R(f(i);f(j))) |
| THM | no_finite_model
|
 ( ( A:Type, R:(A A:Type, R:(A  A A  Prop). Prop).
 (( ((  A) & (Trans x,y:A. R(x;y)) & ( A) & (Trans x,y:A. R(x;y)) & ( x:A. x:A.  y:A. R(x;y)) y:A. R(x;y))
 (& (&  ( ( x:A. R(x;x)) x:A. R(x;x))
 (& Finite(A)) (& Finite(A)) |
| THM | simple_card_cross_assoc
|
(A B B C) ~ ((A C) ~ ((A B) B) C) C) |
| THM | bijtype_ooc_inj_isect_surjtype
|
(A bij B) ~ ((A inj B) ~ ((A inj B) B)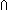 (A onto (A onto B)) B)) |
| THM | ifthenelse_distr_subtype_ooc
|
{x:A| if b P(x) else Q(x) fi } ~ if b P(x) else Q(x) fi } ~ if b {x:A| P(x) } else {x:A| Q(x) } fi {x:A| P(x) } else {x:A| Q(x) } fi |
| THM | card_subset_vs_and
|
{x:{x:A| P(x) }| Q(x) } ~ {x:A| P(x) & Q(x) } |
| THM | card_sum_family_singleton_vs_intseg
|
 a,a': a,a': . a'-a = 1 . a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type{i}). (i:{a..a' Type{i}). (i:{a..a' } } B(i)) ~ ({a: B(i)) ~ ({a: } } B(a))) B(a))) |
| THM | card1_iff_inhabited_uniquely
|
(A ~  1) 1)   ( ( ! ! A) A) |
| THM | card_void_dom_fun_unit
|
( 0 0  A) ~ A) ~  1 1 |
| THM | nsub_delete
|
 k: k: , j: , j: k, m: k, m: . m = k-1 . m = k-1   ({i: ({i: k| k|  i = j } ~ i = j } ~  m) m) |
| THM | nsub_delete_rw
|
 k: k: , j: , j: k. {i: k. {i: k| k|  i = j } ~ i = j } ~  (k-1) (k-1) |
| THM | card_nsub_inj_vs_lopped
|
The cardinality of injections on a finite nonempty domain in terms of injections on a domain one smaller.
The number ways to order a distinct objects from among b is b times the number of ways to order a-1 distinct objects from among b-1.
 a,b: a,b:  . ( . ( a inj a inj  b) ~ ( b) ~ ( b b ( ( (a-1) inj (a-1) inj  (b-1))) (b-1))) |
| THM | card_prod_family_singleton_elim
|
(i:{a:A}  B(i)) ~ B(a) B(i)) ~ B(a) |
| THM | card_prod_family_intseg_singleton_elim
|
 a,a': a,a': . a'-a = 1 . a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type{i}). (i:{a..a' Type{i}). (i:{a..a' } }  B(i)) ~ B(a)) B(i)) ~ B(a)) |
| THM | subset_sq_remove_card
|
{x:A|  B(x) } ~ {x:A| B(x) } B(x) } ~ {x:A| B(x) } |
| THM | one_one_corr_2_weakening_wrt
|
A = B   (A ~ B) (A ~ B) |
| THM | card0_iff_uninhabited
|
A class has zero members just when it doesn't have any.
(A ~  0) 0)    ( (  A) A) |
| THM | card_sum_family_singleton_elim
|
 B:({a:A} B:({a:A}  Type). (i:{a:A} Type). (i:{a:A} B(i)) ~ B(a) B(i)) ~ B(a) |
| THM | card_sum_family_intseg_singleton_elim
|
 a,a': a,a': . a'-a = 1 . a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type{i}). (i:{a..a' Type{i}). (i:{a..a' } } B(i)) ~ B(a)) B(i)) ~ B(a)) |
| def | one_one_corr_fams
|
One-to-one correspondence between index families of classes.
(x:A. B(x)) ~ (x':A'. B'(x'))
==  f:(A f:(A  A'), g:(A' A'), g:(A'  A), F:(x:A A), F:(x:A  B(x) B(x)  B'(f(x))), G:(x:A B'(f(x))), G:(x:A  B'(f(x)) B'(f(x))  B(x)). B(x)).
== InvFuns(A;A';f;g) & ( u:A. InvFuns(B(u);B'(f(u));F(u);G(u))) u:A. InvFuns(B(u);B'(f(u));F(u);G(u))) |
| THM | one_one_corr_fams_refl
|
(x:A. B(x)) ~ (x:A. B(x)) |
| THM | decidable_vs_unique_nsub2
|
Dec(P)   ( ( !i: !i: 2. if i= 2. if i= 0 0 P else P else  P fi) P fi) |
| THM | least_exists
|
 k: k: , P:{P:( , P:{P:( k k  Prop)| Prop)|  i: i: k. P(i) }. k. P(i) }.
( i: i: k. Dec(P(i))) k. Dec(P(i)))   ( (  {i: {i: k| P(i) & ( k| P(i) & ( j: j: i. i.  P(j)) }) P(j)) }) |
| THM | least_exists2
|
Existence of a least number having a given property.
 P:{P:( P:{P:(   Prop)| Prop)|  i: i: . P(i) }. . P(i) }.
( i: i: . Dec(P(i))) . Dec(P(i)))   ( (  {i: {i: | P(i) & ( | P(i) & ( j: j: . j<i . j<i    P(j)) }) P(j)) }) |
| def | is_one_one_corr
|
(function f is a one-to-one correspondence)
f is 1-1 corr ==  g:(B g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g) |
| def | is_permutation
|
f is permutation on A == f is 1-1 corr |
| def | union_to_sigma
|
union_to_sigma(e) == InjCase(e; a. <0,a>; b. <1,b>) |
| def | sigma_to_union
|
sigma_to_union(e) == e/i,u. if i= 0 0 inl(u) else inr(u) fi inl(u) else inr(u) fi |
| def | inv_pair
|
(the inverse function pairs between A and B)
A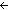  B == {fg:((A B == {fg:((A  B) B) (B (B  A))| fg/f,g. InvFuns(A;B;f;g) } A))| fg/f,g. InvFuns(A;B;f;g) } |
| THM | inv_pair_iff_ooc
|
(  (A (A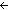  B)) B))   (A ~ B) (A ~ B) |
| def | fin_enum
|
(the finite enumerations of A)
fin_enum(A) == k:   k k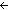  A A |
| THM | factorial_via_intseg_zero
|
0!   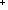 |
| THM | factorial_via_intseg_step
|
 k,n: k,n: . k = n+1 . k = n+1   k! = k k! = k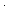 n! n!   |
| THM | factorial_via_intseg_step_rw
|
 k: k: 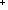 . k! = k . k! = k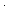 (k-1)! (k-1)!   |
| def | unboundedly_infinite
|
(one can find any number of members of A)
Unbounded(A) ==  k: k: . .   ( ( k inj k inj A) A) |
| def | productively_infinite
|
(there is an infinite (omega) sequence of distinct members of A)
Infinite(A) ==   ( ( inj inj A) A) |
| THM | unboundedly_imp_productively_infinite
|
Infinite(A)   Unbounded(A) Unbounded(A) |
| def | Dedekind_infinite
|
Dedekind's formulation of infinite class
(A can be mapped 1-1 into a proper subpart of itself)
Dedekind-Infinite(A) ==  a:A, f:(A a:A, f:(A  A). Inj(A; A; f) & A). Inj(A; A; f) &  ( ( x:A. f(x) = a) x:A. f(x) = a) |
| THM | ndiff_bound
|
 b,a: b,a: . b . b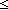 (b -- a)+a (b -- a)+a |
| THM | eq_mem_is_ax
|
 a,a':A, x:(a = a'). x = * a,a':A, x:(a = a'). x = * |
| THM | comp_preserves_inj
|
Composing injections gives an injection.
Inj(A; B; g)   Inj(B; C; f) Inj(B; C; f)   Inj(A; C; f o g) Inj(A; C; f o g) |
| THM | comp_preserves_surj
|
Composing surjections gives a surjection.
Surj(A; B; g)   Surj(B; C; f) Surj(B; C; f)   Surj(A; C; f o g) Surj(A; C; f o g) |
| THM | surjection_type_surjection
|
 f:(A onto f:(A onto B), a: B), a: . .  a onto a onto A A   (B Discrete) (B Discrete)   Surj(A; B; f) Surj(A; B; f) |
| THM | surjection_type_nsub_surjection
|
 f:( f:( a onto a onto  b). Surj( b). Surj( a; a;  b; f) b; f) |
| THM | inv_pair_functionality_wrt_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   ((A ((A  B) ~ (A' B) ~ (A'  B')) B')) |
| THM | one_one_corr_fams_trans
|
One-to-one correspondence between indexed families of classes is transitive.
 A:Type, A',A'':Type, B:(A A:Type, A',A'':Type, B:(A  Type), B':(A' Type), B':(A'  Type), B'':(A'' Type), B'':(A''  Type). Type).
(x:A. B(x)) ~ (x':A'. B'(x'))
 
(x':A'. B'(x')) ~ (x'':A''. B''(x''))   (x:A. B(x)) ~ (x'':A''. B''(x'')) (x:A. B(x)) ~ (x'':A''. B''(x'')) |
| THM | comp_preserves_bij
|
Composing bijections gives a bijection.
Bij(A; B; g)   Bij(B; C; f) Bij(B; C; f)   Bij(A; C; f o g) Bij(A; C; f o g) |
| THM | one_one_corr_rel_vs_invfuns
|
Equivalence of one-one correspondence and existence of inverses
 R:(A R:(A  B B  Prop). Prop).
(1-1-Corr x:A,y:B. R(x;y))
 
( f:(A f:(A  B), g:(B B), g:(B  A). A).
(InvFuns(A;B;f;g) & ( x:A, y:B. R(x;y) x:A, y:B. R(x;y)   y = f(x) & x = g(y))) y = f(x) & x = g(y))) |
| THM | card_split_prod_intseg_family_decbl
|
( x:A. Dec(P(x))) x:A. Dec(P(x)))   ((x:A ((x:A  B(x)) ~ ((x:A st P(x) B(x)) ~ ((x:A st P(x)  B(x)) B(x)) (x:A st (x:A st  P(x) P(x)  B(x)))) B(x)))) |
| THM | finite_choice
|
Principle of finite choice. The function can be constructed explicitly without appeal to the Axiom of Choice.
 k: k: , Q:( , Q:( k k  A A  Prop). ( Prop). ( x: x: k. k.  y:A. Q(x;y)) y:A. Q(x;y))   ( ( f:( f:( k k  A). A).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) |
| THM | dep_finite_choice
|
Principle of dependent finite choice. The function can be constructed explicitly without appeal to the Dependent Axiom of Choice.
 k: k: , B:( , B:( k k  Type), Q:(x: Type), Q:(x: k k  B(x) B(x)  Prop). Prop).
( x: x: k. k.  y:B(x). Q(x;y)) y:B(x). Q(x;y))   ( ( f:(x: f:(x: k k  B(x)). B(x)).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) |
| THM | inv_funs_2_sym
|
Being mutual inverses is symmetric.
InvFuns(A;B;f;g)   InvFuns(B;A;g;f) InvFuns(B;A;g;f) |
| THM | invfuns_are_surj
|
Mutually inverse functions are surjections.
InvFuns(A;B;f;g)   Surj(A; B; f) & Surj(B; A; g) Surj(A; B; f) & Surj(B; A; g) |
| THM | surjection_type_functionality_wrt_ooc
|
(A ~ A')   (B ~ B') (B ~ B')   ((A onto ((A onto B) ~ (A' onto B) ~ (A' onto B')) B')) |
| THM | one_one_corr_fams_sym
|
 B:(A B:(A  Type), B':(A' Type), B':(A'  Type). Type).
(x:A. B(x)) ~ (x':A'. B'(x'))   (x':A'. B'(x')) ~ (x:A. B(x)) (x':A'. B'(x')) ~ (x:A. B(x)) |
| THM | fun_with_inv2_is_inj_rev
|
InvFuns(A;B;f;g)   Inj(B; A; g) Inj(B; A; g) |
| THM | ooc_preserves_dededkind_inf
|
(A ~ B)   Dedekind-Infinite(A) Dedekind-Infinite(A)   Dedekind-Infinite(B) Dedekind-Infinite(B) |
| THM | invfuns_are_inj
|
Mutually inverse functions are injections.
InvFuns(A;B;f;g)   Inj(A; B; f) & Inj(B; A; g) Inj(A; B; f) & Inj(B; A; g) |
| THM | injection_type_functionality_wrt_ooc
|
(A ~ A')   (B ~ B') (B ~ B')   ((A inj ((A inj B) ~ (A' inj B) ~ (A' inj B')) B')) |
| THM | fun_with_inv2_is_surj_rev
|
InvFuns(A;B;f;g)   Surj(B; A; g) Surj(B; A; g) |
| THM | one_one_corr_is_equiv_rel
|
EquivRel X,Y:Type. X ~ Y |
| THM | iff_weakening_wrt_one_one_corr_2
|
(A ~ B)   (A (A   B) B) |
| THM | inhabited_functionality_wrt_one_one_corr
|
(A ~ B)   (( ((  A) A)   ( (  B)) B)) |
| THM | one_one_corr_2_functionality_wrt_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   ((A ~ B) ((A ~ B)   (A' ~ B')) (A' ~ B')) |
| THM | one_one_corr_2_reflex
|
A ~ A |
| THM | one_one_corr_2_inversion
|
(A ~ B)   (B ~ A) (B ~ A) |
| THM | one_one_corr_2_transitivity
|
(A ~ B)   (B ~ C) (B ~ C)   (A ~ C) (A ~ C) |
| COM | one_one_corr_via_bijection
|
One-to-One Correspondence via Bijection
... |
| COM | one_one_corr_and_bij_thm
|
One-to-One Correspondence: equivalence of two characterizations.
... |
| THM | inv_funs_2_unique
|
A function has at most one inverse.
InvFuns(A;B;f;g)   InvFuns(A;B;f;h) InvFuns(A;B;f;h)   g = h g = h |
| THM | left_inv_of_surj_is_right_inv
|
A function that cancels a surjection is also cancelled by it.
 g:(B g:(B  A). Surj(A; B; f) A). Surj(A; B; f)   ( ( x:A. g(f(x)) = x) x:A. g(f(x)) = x)   ( ( y:B. f(g(y)) = y) y:B. f(g(y)) = y) |
| THM | parallel_conjunct_imp
|
(A   C) C)   (B (B   D) D)   A & B A & B   C & D C & D |
| THM | fun_with_inv2_is_bij
(Proof Gloss) |
InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) |
| THM | fun_with_inv2_is_bij_rev
|
InvFuns(A;B;f;g)   Bij(B; A; g) Bij(B; A; g) |
| THM | comp_id_r_version2
|
 f:(A f:(A  B). f o Id = f B). f o Id = f  A A  B B |
| THM | comp_id_l_version2
|
 f:(A f:(A  B). Id o f = f B). Id o f = f  A A  B B |
| THM | comp_assoc_version2
|
 f:(A f:(A  B), g:(B B), g:(B  C), h:(C C), h:(C  D). h o (g o f) = (h o g) o f D). h o (g o f) = (h o g) o f  A A  D D |
| THM | eta_conv_version2
|
 f:(A f:(A  B). ( B). ( x.f(x)) = f x.f(x)) = f |
| THM | fun_with_inv_is_bij_version2
|
 f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) |
| THM | bij_imp_exists_inv_version2
|
Bijections have inverses.
 f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) |
| THM | bij_iff_1_1_corr_version2
|
( f:(A f:(A  B). Bij(A; B; f)) B). Bij(A; B; f))   (A ~ B) (A ~ B) |
| THM | int_ooc_nat
|
There are as many non-negative integers as integers.
 ~ ~  |
| THM | unb_inf_not_fin
|
Unbounded(A)    Finite(A) Finite(A) |
| THM | infinite_imp_nonfinite
|
Infinite(A)    Finite(A) Finite(A) |
| THM | ooc_preserves_unb_inf
|
(A ~ B)   Unbounded(A) Unbounded(A)   Unbounded(B) Unbounded(B) |
| THM | ooc_preserves_infiniteness
|
(A ~ B)   Infinite(A) Infinite(A)   Infinite(B) Infinite(B) |
| THM | bij_iff_1_1_corr_version2a
|
( f:(A f:(A  B). Bij(A; B; f)) B). Bij(A; B; f))   (B ~ A) (B ~ A) |
| THM | negnegelim_imp_notfin_imp_unb_inf
|
( P:Prop. P:Prop.   P P   P) P)   ( ( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A)) |
| THM | nsub_not_infinite
|
 k: k: . .  Infinite( Infinite( k) k) |
| THM | absurd_nonfin_imp_unb_inf
|
( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A))   ( ( D:Type. D:Type.   ( (  D) D)   ( (  D)) D)) |
| THM | nonfin_eqv_unb_inf_iff_negnegelim
|
( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A))   ( ( P:Prop. P:Prop.   P P   P) P) |
| THM | absurd_nonfinite_imp_infinite
|
( A:Type. A:Type.  Finite(A) Finite(A)   Infinite(A)) Infinite(A))   ( ( D:Type. D:Type.   ( (  D) D)   ( (  D)) D)) |
| THM | not_nat_occ_natfuns
|
The infinite sequences of numbers cannot be paired one-to-one with the numbers themselves. (Cantor)
 (( ((    ) ~ ) ~  ) ) |
| THM | counting_is_unique
(Proof Gloss) |
Any way of counting a finite class produces the same number.
(A ~  m) m)   (A ~ (A ~  k) k)   m = k m = k |
| THM | fin_card_vs_nat_eq
|
 a,b: a,b: . ( . ( a ~ a ~  b) b)   a = b a = b |
| THM | nat_not_finite
|
 Finite( Finite( ) ) |
| THM | partition_type
|
 P:(A P:(A  B B  Prop). ( Prop). ( x:A. x:A.  !y:B. P(x;y)) !y:B. P(x;y))   (A ~ (y:B (A ~ (y:B {x:A| P(x;y) })) {x:A| P(x;y) })) |
| THM | bij_imp_exists_inv2
|
Bijections have inverses.
 f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) |
| THM | bij_iff_is_1_1_corr
|
Bijections and one-one correspondence functions are the same.
Bij(A; B; f)   f is 1-1 corr f is 1-1 corr |
| THM | one_one_corr_fams_if_one_one_corr_B
|
( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   (x:A. B(x)) ~ (x:A. B'(x)) (x:A. B(x)) ~ (x:A. B'(x)) |
| THM | one_one_corr_fams_if_bij_A
|
 g:(A' g:(A'  A). Bij(A'; A; g) A). Bij(A'; A; g)   (x:A. B(x)) ~ (x':A'. B(g(x'))) (x:A. B(x)) ~ (x':A'. B(g(x'))) |
| THM | one_one_corr_fams_indep_if_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   (:A. B) ~ (:A'. B') (:A. B) ~ (:A'. B') |
| THM | union_functionality_wrt_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   ((A+B) ~ (A'+B')) ((A+B) ~ (A'+B')) |
| def | seq_nil
|
Nil(i) == i |
| def | seq_cons
|
[x/ xs](i) == if i= 0 0 x else xs(i-1) fi x else xs(i-1) fi |
| THM | card_product_swap
|
(A B) ~ (B B) ~ (B A) A) |
| THM | card_settype
|
Bij(A; A'; f)   ( ( x:A. B(x) x:A. B(x)   B'(f(x))) B'(f(x)))   ({x:A| B(x) } ~ {x:A'| B'(x) }) ({x:A| B(x) } ~ {x:A'| B'(x) }) |
| THM | card_settype_sq
|
Bij(A; A'; f)   ( ( x:A. x:A. 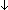 B(x) B(x)   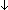 B'(f(x))) B'(f(x)))   ({x:A| B(x) } ~ {x:A'| B'(x) }) ({x:A| B(x) } ~ {x:A'| B'(x) }) |
| THM | set_functionality_wrt_one_one_corr_n_pred2
|
( x:A. B(x) x:A. B(x)   B'(x)) B'(x))   ({x:A| B(x) } ~ {x:A| B'(x) }) ({x:A| B(x) } ~ {x:A| B'(x) }) |
| THM | set_functionality_wrt_one_one_corr_n_pred
|
( x:A. x:A. 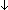 B(x) B(x)   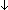 B'(x)) B'(x))   ({x:A| B(x) } ~ {x:A| B'(x) }) ({x:A| B(x) } ~ {x:A| B'(x) }) |
| THM | card_sigma
|
(x:A. B(x)) ~ (x:A'. B'(x))   ((x:A ((x:A B(x)) ~ (x:A' B(x)) ~ (x:A' B'(x))) B'(x))) |
| THM | product_functionality_wrt_one_one_corr_B
|
 B,B':(A B,B':(A  Type). ( Type). ( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   ((x:A ((x:A B(x)) ~ (x:A B(x)) ~ (x:A B'(x))) B'(x))) |
| THM | card_quotient
|
(q:A/E {x:A| q = x {x:A| q = x  A/E }) ~ A A/E }) ~ A |
| THM | product_functionality_wrt_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   ((A ((A B) ~ (A' B) ~ (A' B')) B')) |
| THM | card_split_prod_intseg_family
|
 a,b: a,b: , c:{a...b}, B:({a..b , c:{a...b}, B:({a..b } }  Type). Type).
(i:{a..b } }  B(i)) ~ ((i:{a..c B(i)) ~ ((i:{a..c } }  B(i)) B(i)) (i:{c..b (i:{c..b } }  B(i))) B(i))) |
| THM | union_sigma_inverses
|
InvFuns(A+B;i: 2 2 if i= if i=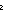 0 0 A else B fi;union_to_sigma;sigma_to_union) A else B fi;union_to_sigma;sigma_to_union) |
| THM | card_union_swap
|
(A+B) ~ (B+A) |
| THM | card_union_vs_sigma
|
(A+B) ~ (i: 2 2 if i= if i=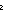 0 0 A else B fi) A else B fi) |
| THM | card_split_decbl
|
( x:A. Dec(P(x))) x:A. Dec(P(x)))   (A ~ ({x:A| P(x) }+{x:A| (A ~ ({x:A| P(x) }+{x:A|  P(x) })) P(x) })) |
| THM | card_sigma_st_dom
|
 B:(A B:(A  Type), P:(A Type), P:(A  Prop). (i:{i:A| P(i) } Prop). (i:{i:A| P(i) } B(i)) ~ {v:(i:A B(i)) ~ {v:(i:A B(i))| P(v/x,y. x) } B(i))| P(v/x,y. x) } |
| THM | card_split_sigma_dom_decbl
|
 B:(A B:(A  Type), P:(A Type), P:(A  Prop). Prop).
( i:A. Dec(P(i))) i:A. Dec(P(i)))
 
((i:A B(i)) ~ ((i:{i:A| P(i) } B(i)) ~ ((i:{i:A| P(i) } B(i))+(i:{i:A| B(i))+(i:{i:A|  P(i) } P(i) } B(i)))) B(i)))) |
| THM | card_nsub0_union
|
( 0+A) ~ A 0+A) ~ A |
| THM | card_nsub0_union_2
|
(A+ 0) ~ A 0) ~ A |
| THM | card_split_decbl_squash
|
( x:A. Dec( x:A. Dec(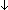 P(x))) P(x)))   (A ~ ({x:A| P(x) }+{x:A| (A ~ ({x:A| P(x) }+{x:A|  P(x) })) P(x) })) |
| THM | card_split_sum_intseg_family
|
 a,b: a,b: , c:{a...b}, B:({a..b , c:{a...b}, B:({a..b } }  Type). Type).
(i:{a..b } } B(i)) ~ ((i:{a..c B(i)) ~ ((i:{a..c } } B(i))+(i:{c..b B(i))+(i:{c..b } } B(i))) B(i))) |
| THM | card_split_end_sum_intseg_family
|
 a,b: a,b: , B:({a..b , B:({a..b } }  Type). Type).
a<b   ((i:{a..b ((i:{a..b } } B(i)) ~ ((i:{a..(b-1) B(i)) ~ ((i:{a..(b-1) } } B(i))+B(b-1))) B(i))+B(b-1))) |
| THM | card_pi
|
(x:A. B(x)) ~ (x:A'. B'(x))   ((x:A ((x:A  B(x)) ~ (x:A' B(x)) ~ (x:A'  B'(x))) B'(x))) |
| THM | function_functionality_wrt_one_one_corr_B
|
 B,B':(A B,B':(A  Type). ( Type). ( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   ((x:A ((x:A  B(x)) ~ (x:A B(x)) ~ (x:A  B'(x))) B'(x))) |
| THM | function_functionality_wrt_one_one_corr
|
(A ~ A')   (B ~ B') (B ~ B')   ((A ((A  B) ~ (A' B) ~ (A'  B')) B')) |
| THM | card_curry_simple
|
(A B B  C) ~ (A C) ~ (A  B B  C) C) |
| THM | card_curry
|
(z:(x:A B(x)) B(x))  C(z)) ~ (x:A C(z)) ~ (x:A  y:B(x) y:B(x)  C(<x,y>)) C(<x,y>)) |
| THM | card_sigma_distr
|
(xy:(x:A B(x)) B(x)) C(xy)) ~ (x:A C(xy)) ~ (x:A y:B(x) y:B(x) C(<x,y>)) C(<x,y>)) |
| THM | intseg_void
|
 a,b: a,b: . b . b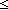 a a   (Void ~ {a..b (Void ~ {a..b }) }) |
| THM | nsub_void
|
Void ~  0 0 |
| THM | intseg_shift
|
 a,b,a',b': a,b,a',b': . b-a = b'-a' . b-a = b'-a'   ({a..b ({a..b } ~ {a'..b' } ~ {a'..b' }) }) |
| THM | intseg_shift_by
|
 a: a: , b,c: , b,c: . {a..b . {a..b } ~ {(a+c)..(b+c) } ~ {(a+c)..(b+c) } } |
| THM | nsub_unit
|
Unit ~  1 1 |
| THM | nsub_bool
|
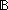 ~ ~  2 2 |
| THM | nsub_intseg
|
 c,a: c,a: , b: , b: . c = b-a . c = b-a   ({a..b ({a..b } ~ } ~  c) c) |
| THM | nsub_intseg_rw
|
 a,b: a,b: . {a..b . {a..b } ~ } ~  (b-a) (b-a) |
| THM | intiseg_intseg
|
 a,b',b: a,b',b: . b = b'+1 . b = b'+1   ({a...b'} ~ {a..b ({a...b'} ~ {a..b }) }) |
| THM | intiseg_intseg_plus
|
 a: a: , b: , b: . {a...b} ~ {a..(b+1) . {a...b} ~ {a..(b+1) } } |
| THM | nsub_intiseg_rw
|
 a,b: a,b: . {a...b} ~ . {a...b} ~  (1+b-a) (1+b-a) |
| THM | intseg_split
|
 a,b: a,b: , c:{a...b}. ({a..c , c:{a...b}. ({a..c }+{c..b }+{c..b }) ~ {a..b }) ~ {a..b } } |
| THM | nsub_add
|
 c,a,b: c,a,b: . a+b = c . a+b = c     (( (( a+ a+ b) ~ b) ~  c) c) |
| THM | nsub_mul
|
 a,b,c: a,b,c: . a . a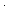 b = c b = c   (( (( a a  b) ~ b) ~  c) c) |
| THM | nsub_mul_rw
|
 a,b: a,b: . ( . ( a a  b) ~ b) ~  (a (a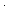 b) b) |
| THM | mul_assoc_from_cross_assoc
|
 a,b,c: a,b,c: . a . a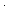 (b (b c) = (a c) = (a b) b) c c |
| THM | finite_indep_sum_card
|
 a,b: a,b: . (A ~ . (A ~  a) a)   (B ~ (B ~  b) b)   ((A ((A B) ~ B) ~  (a (a b)) b)) |
| THM | nsub_inj_factorial2
|
Relevant to permutation counting problems since these injections are the finite permutations.
( b inj b inj  b) ~ b) ~  (b!) (b!) |
| THM | nsub_inj_factorial_tail
|
Relevant to so-called permutation counting problems since these injections are the ways to order a distinct values chosen from a total of b values.
( a inj a inj  b) ~ b) ~  (b!a) (b!a) |
| THM | nsub_inj_factorial
|
A more direct proof of this fact is in nsub inj factorial2.
( k inj k inj  k) ~ k) ~  (k!) (k!) |
| THM | card_pi_vs_nsub_pi
|
The size of the general product space (whose members are functions) of a finite family of finite classes is the integer product of those classes' sizes.
 a: a: , b:( , b:( a a   ). (i: ). (i: a a   b(i)) ~ b(i)) ~  ( (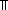 i: i: a. b(i)) a. b(i)) |
| THM | card_fun_vs_nsub_exp
|
Corollary to card pi vs nsub pi
 a,b: a,b: . ( . ( a a   b) ~ b) ~  (b (b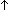 a) a) |
| THM | exp_exp_reduce1
|
 a,b,c: a,b,c: . c . c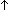 (a (a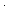 b) = (c b) = (c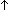 b) b)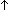 a a |
| THM | exp_exp_reduce2
|
 a,b,c: a,b,c: . c . c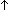 (a (a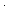 b) = (c b) = (c a) a) b b |
| THM | card_curry_simple2
|
(A B B  C) ~ (B C) ~ (B  A A  C) C) |
| THM | nsub_add_rw
|
The size of the disjoint union of two finite classes is the sum of those classes' sizes.
 a,b: a,b: . ( . ( a+ a+ b) ~ b) ~  (a+b) (a+b) |
| THM | card_sigma_vs_nsub_sigma
|
The size of a general sum (whose members are pairs) of a finite family of finite classes is the integer sum of those classes' sizes.
 a: a: , b:( , b:( a a   ). (i: ). (i: a a  b(i)) ~ b(i)) ~  ( ( i: i: a. b(i)) a. b(i)) |
| THM | inv_pair_inv
|
(A  B) ~ (A ~ B) B) ~ (A ~ B) |
| THM | inv_pair_inv2
|
(  (A (A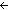  B)) ~ (A ~ B) B)) ~ (A ~ B) |
| def | next_nat_pair
|
How to step from pair to pair exhaustively
next_nat_pair(xy) == xy/x,y. if y=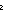 0 0 <0,x+1> else <x+1,y-1> fi <0,x+1> else <x+1,y-1> fi |
| THM | next_nat_pair_not_zeroes
|
The zero-zero pair does not succeed any other.
 xy:( xy:(   ). ).  <0,0> = next_nat_pair(xy) <0,0> = next_nat_pair(xy)     |
| THM | next_nat_pair_inj
|
Inj(   ; ;    ; next_nat_pair) ; next_nat_pair) |
| def | prev_nat_pair
|
Reverses next nat pair
prev_nat_pair(xy) == xy/x,y. if x=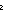 0 0 <y-1,0> else <x-1,y+1> fi <y-1,0> else <x-1,y+1> fi |
| THM | next_nat_pair_vs_prev_nat_pair
|
InvFuns(   ;{xy:( ;{xy:(   )| )|  xy = <0,0> xy = <0,0>     };next_nat_pair;prev_nat_pair) };next_nat_pair;prev_nat_pair) |
| def | nat_to_nat_pair
|
(i steps of next_nat_pair from <0,0>)
nat_to_nat_pair(i) == next_nat_pair{ i}(<0,0>) i}(<0,0>) |
| THM | nat_to_nat_pair_inj
|
Inj( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) |
| THM | nat_to_nat_pair_surj
|
Surj( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) |
| THM | nat_to_nat_pair_bij
|
Bij( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) |
| THM | card_nat_vs_nat_nat
|
The ordered pairs of natural numbers can be placed in one-to-one correspondence with the natural numbers. (Cantor)
(   ) ~ ) ~  |
| THM | card_nat_vs_nat_tuple
|
The k-tuples of natural numbers can be placed in one-to-one correspondence with the natural numbers theselves.
 k: k: 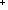 . ( . ( k k   ) ~ ) ~  |
| THM | card_nat_vs_nat_tuples
|
The finite nonempty sequences of natural numbers can be placed in one-one correspondence with the natural numbers themselves.
(k: 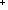   k k   ) ~ ) ~  |
| THM | card_nat_vs_nat_tuples_all
|
The finite sequences of natural numbers can be placed in one-one correspondence with the natural numbers themselves.
(k:   k k   ) ~ ) ~  |
| THM | compose_iter_zero
|
 f:(A f:(A  A), x:A. f{ A), x:A. f{ 0}(x) = x 0}(x) = x |
| THM | compose_iter_zero_id
|
 f:(A f:(A  A). f{ A). f{ 0} = Id 0} = Id |
| THM | compose_iter_once
|
 f:(A f:(A  A). f{ A). f{ 1} = f 1} = f |
| THM | compose_iter_pos
|
 f:(A f:(A  A), i: A), i: 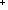 , x:A. f{ , x:A. f{ i}(x) = f(f{ i}(x) = f(f{ i-1}(x)) i-1}(x)) |
| THM | compose_iter_point_id
|
 f:(A f:(A  A), u:A. f(u) = u A), u:A. f(u) = u   ( ( i: i: . f{ . f{ i}(u) = u) i}(u) = u) |
| THM | compose_iter_pos_comp
|
 f:(A f:(A  A), i: A), i: 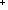 . f{ . f{ i} = f o f{ i} = f o f{ i-1} i-1} |
| THM | compose_iter_id
|
 i: i: . Id{ . Id{ i} = Id i} = Id  A A  A A |
| THM | compose_iter_sum
|
 x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i}(f{ i}(f{ j}(x)) = f{ j}(x)) = f{ k}(x) k}(x) |
| THM | compose_iter_sum_comp
|
 f:(A f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i} o f{ i} o f{ j} = f{ j} = f{ k} k} |
| THM | compose_iter_sum_rw
|
 x:A, f:(A x:A, f:(A  A), k: A), k: , i:{0...k}. f{ , i:{0...k}. f{ k}(x) = f{ k}(x) = f{ i}(f{ i}(f{ k-i}(x)) k-i}(x)) |
| THM | compose_iter_sum_comp_rw
|
 f:(A f:(A  A), k: A), k: , i:{0...k}. f{ , i:{0...k}. f{ k} = f{ k} = f{ i} o f{ i} o f{ k-i} k-i} |
| THM | compose_iter_prod
|
 x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i . k = i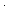 j j   f{ f{ i}{ i}{ j}(x) = f{ j}(x) = f{ k}(x) k}(x)  A A |
| THM | compose_iter_prod2
|
 x:A, f:(A x:A, f:(A  A), i,j: A), i,j: . f{ . f{ i}{ i}{ j}(x) = f{ j}(x) = f{ i i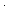 j}(x) j}(x) |
| THM | compose_iter_pos2
|
 f:(A f:(A  A), i: A), i: 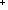 , x:A. f{ , x:A. f{ i}(x) = f{ i}(x) = f{ i-1}(f(x)) i-1}(f(x)) |
| THM | compose_iter_pos_comp2
|
 f:(A f:(A  A), i: A), i: 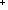 . f{ . f{ i} = f{ i} = f{ i-1} o f i-1} o f |
| THM | compose_iter_injection
|
Iteration of an injection is an injection.
Inj(A; A; f)   ( ( i: i: . Inj(A; A; f{ . Inj(A; A; f{ i})) i})) |
| THM | compose_iter_inj_cycles
|
A finite permutation always cycles back on each argument.
 k: k: , f:( , f:( k inj k inj  k), u: k), u: k. k.  i: i: 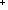 . f{ . f{ i}(u) = u i}(u) = u |
| THM | iter_perm_cycles_uniform
|
Some positive iteration of any finite permutation is the identity function.
 k: k: , f:( , f:( k inj k inj  k). k).  i: i: 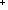 . .  u: u: k. f{ k. f{ i}(u) = u i}(u) = u |
| THM | iter_perm_cycles_uniform2
|
Corollary of iter perm cycles uniform.
Some positive iteration of any finite permutation is the identity function.
 k: k: , f:( , f:( k inj k inj  k). k).  i: i: 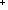 . f{ . f{ i} = Id i} = Id   k k   k k |
| THM | compose_iter_injection2
|
 f:(A inj f:(A inj A), i: A), i: . f{ . f{ i} i}  A inj A inj A A |
| THM | compose_iter_surjection
|
Iteration of a surjection is a surjection.
Surj(A; A; f)   ( ( i: i: . Surj(A; A; f{ . Surj(A; A; f{ i})) i})) |
| THM | compose_iter_bijection
|
Iteration of a bijection is a bijection.
Bij(A; A; f)   ( ( i: i: . Bij(A; A; f{ . Bij(A; A; f{ i})) i})) |
| THM | compose_iter_inverses
|
InvFuns(A;A;f;g)   ( ( i: i: . InvFuns(A;A;f{ . InvFuns(A;A;f{ i};g{ i};g{ i})) i})) |
| THM | dedekind_inf_imp_inf
|
Dedekind-Infinite(A)   Infinite(A) Infinite(A) |
| THM | dededing_imp_unb_inf
|
Dedekind-Infinite(A)   Unbounded(A) Unbounded(A) |
| THM | dedekind_imp_nonfin
|
Dedekind-Infinite(A)    Finite(A) Finite(A) |
| THM | nsub_surj_imp_a_rev_inj_gen
|
 e:(B e:(B  B B  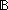 ). ).
IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B). ( B). (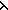 y.least x: y.least x: . (f(x)) e y) . (f(x)) e y)  B inj B inj  a) a) |
| THM | nsub_surj_imp_a_rev_inj
|
 f:( f:( a onto a onto  b). ( b). (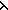 y.least x: y.least x: . f(x)= . f(x)=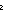 y) y)   b inj b inj  a a |
| THM | nsub_bij_least_preimage_inverse
|
 f:( f:( a bij a bij  a). InvFuns( a). InvFuns( a; a; a;f; a;f;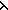 y.least x: y.least x: . f(x)= . f(x)=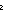 y) y) |
| THM | nsub_surj_imp_a_rev_inj2
|
(  ( ( a onto a onto  b)) b))   ( (  ( ( b inj b inj  a)) a)) |
| THM | surj_typing_imp_le
|
(  ( ( a onto a onto  b)) b))   b b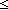 a a |
| THM | nsub_inj_exteq_nsub_surj
|
( k inj k inj  k) =ext ( k) =ext ( k onto k onto  k) k) |
| THM | nsub_surj_exteq_nsub_bij
|
( k onto k onto  k) =ext ( k) =ext ( k bij k bij  k) k) |
| THM | nsub_surj_ooc_nsub_bij
|
( k onto k onto  k) ~ ( k) ~ ( k bij k bij  k) k) |
| THM | nsub_inj_exteq_nsub_bij
|
( k inj k inj  k) =ext ( k) =ext ( k bij k bij  k) k) |
| THM | nsub_inj_ooc_nsub_bij
|
( k inj k inj  k) ~ ( k) ~ ( k bij k bij  k) k) |
| THM | nsub_inj_ooc_nsub_surj
|
( k inj k inj  k) ~ ( k) ~ ( k onto k onto  k) k) |
| THM | nsub_bij_ooc_invpair
|
( a bij a bij  a) ~ ( a) ~ ( a a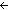   a) a) |
| def | msize
|
The size of a finite multiset.
Msize(f) == 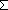 i: i: k. f(i) k. f(i) |
| def | sized_mset
|
(multisets of size k)
 a {k} a {k} T == {p:( T == {p:( a a  T)| Msize(p) = k } T)| Msize(p) = k } |
| def | boolsize
|
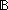 size( size( a)(p) == Msize( a)(p) == Msize(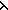 x.if p(x) x.if p(x) 1 else 0 fi) 1 else 0 fi) |
| def | sized_bool
|
 a {k} a {k} 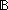 == {p:( == {p:( a a  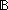 )| )| 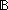 size( size( a)(p) = k } a)(p) = k } |
| THM | card_boolset_vs_mset
|
( a {k} a {k} 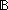 ) ~ ( ) ~ ( a {k} a {k}  2) 2) |
| THM | card_st_vs_msize
|
 f:( f:( a a   2). ( 2). ( i: i: a. P(i) a. P(i)   f(i) = 1 f(i) = 1   2) 2)   ({x: ({x: a| P(x) } ~ a| P(x) } ~  (Msize(f))) (Msize(f))) |
| THM | card_st_vs_boolsize
|
 p:( p:( a a  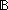 ). {x: ). {x: a| p(x) } ~ a| p(x) } ~  ( (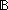 size( size( a)(p)) a)(p)) |
| THM | card_st_sized_bool
|
 p:( p:( a {k} a {k} 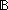 ). {i: ). {i: a| p(i) } ~ a| p(i) } ~  k k |
| def | same_range_sep
|
same_range_sep(A; B) ==   f,g. f,g.  j:B. ( j:B. ( i:A. f(i) = j) i:A. f(i) = j)   ( ( i:A. g(i) = j) i:A. g(i) = j) |
| THM | same_range_sep_eqv
|
EquivRel on A  B, same_range_sep(A; B) B, same_range_sep(A; B) |
| THM | same_range_sep_inj_eqv
|
EquivRel on A inj B, same_range_sep(A; B) B, same_range_sep(A; B) |
| COM | counting_intro2
|
Counting Indirectly - integer ranges.
... |
| COM | counting_intro3
|
Counting Indirectly - ordered pairs
... |
| COM | counting_intro4
|
Counting Indirectly - tuples
... |
| THM | is_list_mem_split
|
 x,a:A, ys:A List. (x x,a:A, ys:A List. (x  a.ys) a.ys)   x = a x = a  (x (x  ys) ys) |
| THM | is_list_mem_null
|
 x:A. (x x:A. (x  nil) nil)   False False |
| def | list_member_type
|
xs == {a:A| a  xs } xs } |
| THM | chessboard_example
|
(AH ~  8) 8)   ((AH ((AH {1...8}) ~ {1...8}) ~  64) 64) |
| COM | counting_intro5
|
Counting indirectly - dependent ordered pairs
... |
| COM | counting_intro6
|
Counting indirectly - basic forms: dependent pairs (2). Counting(dependent pairs - 1)
... |