| 1 |
1. X : Type
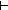  f,g:(X f,g:(X  X). InvFuns(X;X;f;g) X). InvFuns(X;X;f;g)
 | 1 step |
| 2 |
1. X : Type
2. Y : Type
3.  f:(X f:(X  Y), g:(Y Y), g:(Y  X). InvFuns(X;Y;f;g) X). InvFuns(X;Y;f;g)
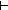  g:(Y g:(Y  X), f:(X X), f:(X  Y). InvFuns(Y;X;g;f) Y). InvFuns(Y;X;g;f)
 | 1 step |
| 3 |
1. X : Type
2. Y : Type
3.  f1:(X f1:(X  Y), g1:(Y Y), g1:(Y  X). InvFuns(X;Y;f1;g1) X). InvFuns(X;Y;f1;g1)
4. Z : Type
5.  f2:(Y f2:(Y  Z), g2:(Z Z), g2:(Z  Y). InvFuns(Y;Z;f2;g2) Y). InvFuns(Y;Z;f2;g2)
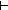  f:(X f:(X  Z), g:(Z Z), g:(Z  X). InvFuns(X;Z;f;g) X). InvFuns(X;Z;f;g)
 | 5 steps |